Andrew Ng. Deep Learning Course 2 Improving Deep Neural Networks 笔记,讲加快学习速度的几种方法,包括 input normalization,batch normalization,mini-batch,Momentum,RMSprop,Adam,learning rate decay 等。
归一化输入
神经网络训练开始前,一般需要对输入数据做归一化处理,把数据归一化为 0 均值、方差为 1 的数据,步骤如下:
- 零均值化
$u={1\over m} \sum^m_{i=1}x^{(i)}$
$x=x-u$ - 方差归一化
$\sigma^2={1\over m}\sum^m_{i=1}x^{(i)}**2$
$x/=\sigma^2$
归一化后的数据分布: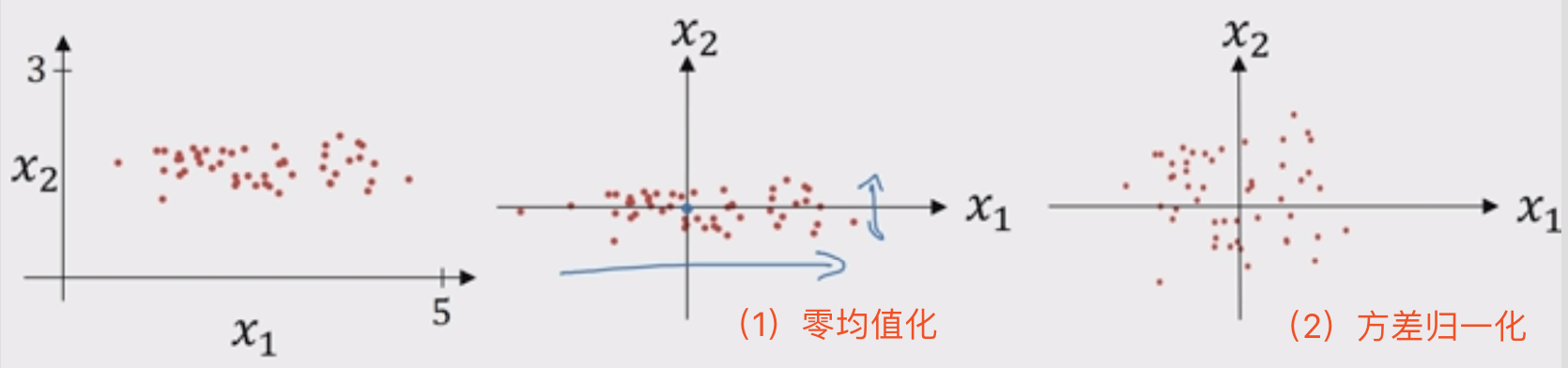
问题是为什么要归一化?或者说什么时候需要归一化?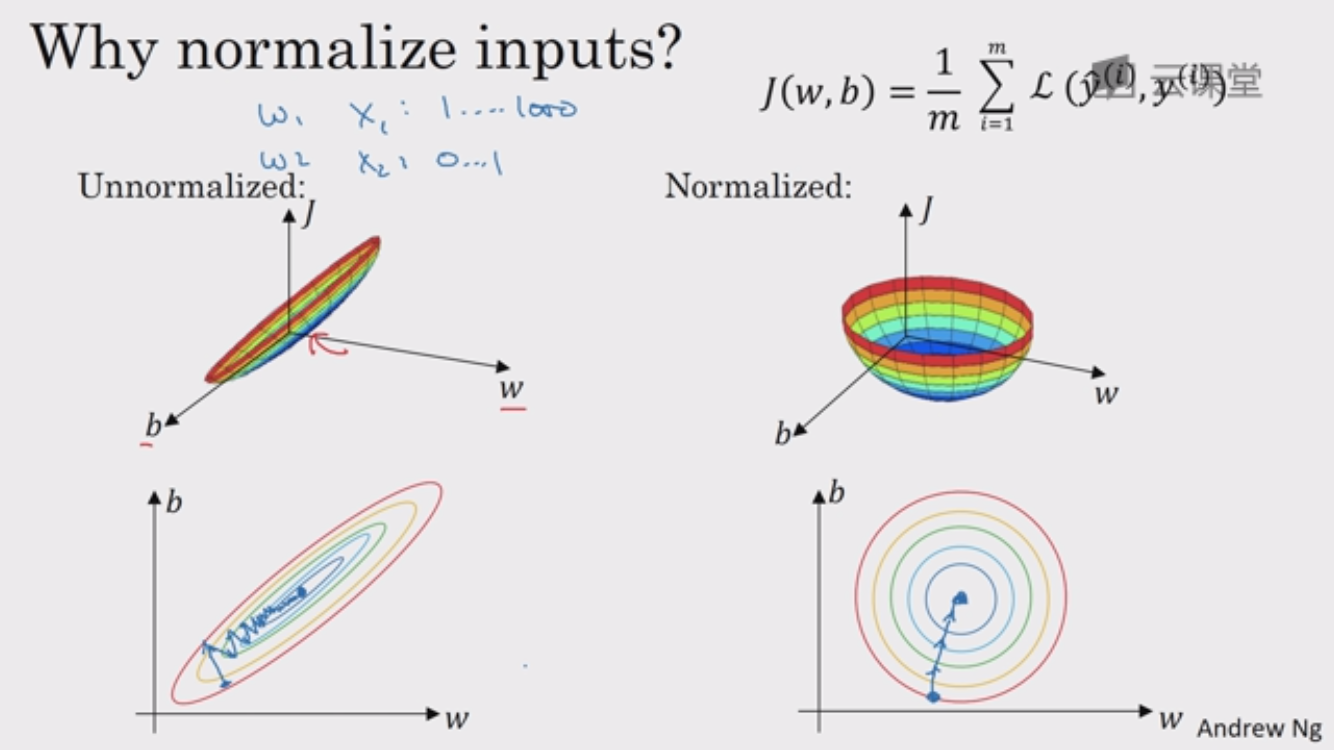
一方面是可以提高学习速率,主要考虑 代价函数,左图代表未归一化的代价函数,右图代表归一化的代价函数,未归一化的代价函数是狭长的,需要更小的学习率,更多的迭代才能到最小值,而归一化后的函数是偏球形的,无论从哪个位置开始,梯度下降法都能够更直接的找到最小值,这样就可以在梯度下降中使用较大步长,优化代价函数 J 更简单快速。
另一个角度是从数据分布角度来看,如果训练数据和测试数据的分布不同,网络的泛化能力会大大降低,另一方面,如果每个 mini-batch 的数据分布不同,网络就需要去学习适应不同的分布,这也会影响学习速度。
当然有些时候并不需要归一化,比如说如果数据本身特征值就在相似范围内,那么归一化就不是很重要,相反,如果特征值的取值范围差别很大,有些特征值从 0 到 1,有些从 1 到 1000,归一化特征就很重要了。
只有输入特征归一化很多时候是不够的,因为除了输入层,后面隐藏层每一层的输入数据分布是一直在发生变化的,比如第二层输入就是由第一层的参数和原始输入计算得到的(z=wx+t, a=g(z)),而第一层的参数在整个训练过程中一直在变化,这必然会引起后面每一层输入数据分布的改变,这种现象(中间层在训练过程中数据分布的改变)又叫做 “Internal Covariate Shift”。
一个直觉就是把归一化不只应用到输入层,也应用到深度隐藏层,这就有了 batch normalization。不过一个区别是,我们不希望 hidden unit value 必须是均值 0 方差 1 的分布(以 sigmoid 为例,如果 z 的均值为 0 方差为 1,就永远处于 sigmoid 线性部分,相当于把这一层网络学到的特征分布给搞坏了,我们不希望这样),所以对每个 mini-batch 求均值、方差、归一化、并学习缩放参数:
$$
\begin{aligned}
u &= {1\over m} \sum^m_{i=1}z^{(i)} \\
\sigma^2 &= {1\over m}\sum^m_{i=1}z^{(i)}**2 \\
z^{(i)}_{norm} &= z^{(i)}-{\mu \over \sqrt{\sigma^2 + \epsilon} } \\
z^{N(i)} &= \gamma z^{(i)}_{norm} + \beta \\
\end{aligned}
$$
$\gamma, \ \beta$ 都是需要学习的参数,每一层都不同,可以用 gradient descent 来学习,$\beta^{[i]}=\beta^{[i]}-\alpha d\beta^{[i]}$。在深度学习框架,一般是把 batch norm 应用于 batch norm layer,直接一行代码就搞定啦。
在测试阶段,每次只有一个样本,$\mu, \sigma$ 哪里来?这需要我们进行估算,可以在网络训练完后运行整个训练集得到 $\mu, \sigma$,也可以在训练时做指数加权平均,来粗略估算 $\mu, \sigma$,然后在测试中使用。
最后提一点,由于 Norm 对 z 加了噪音,所以有轻微的 regularization effect 的效果,迫使后面的单元不会过分依赖前面任何一个单元, 当然越大的 mini-batch size 会减小这种效果。
优化算法
Mini-batch
对整个训练集进行梯度下降时,必须处理完整个训练集后,才能将进行一步梯度下降法,如果把训练集分割为小一点的子训练集(mini-batch),每次同时处理单个 mini-batch,那么 1个 epoch 虽然只遍历了一次训练集,却能够做 5000 个(如下图)梯度下降

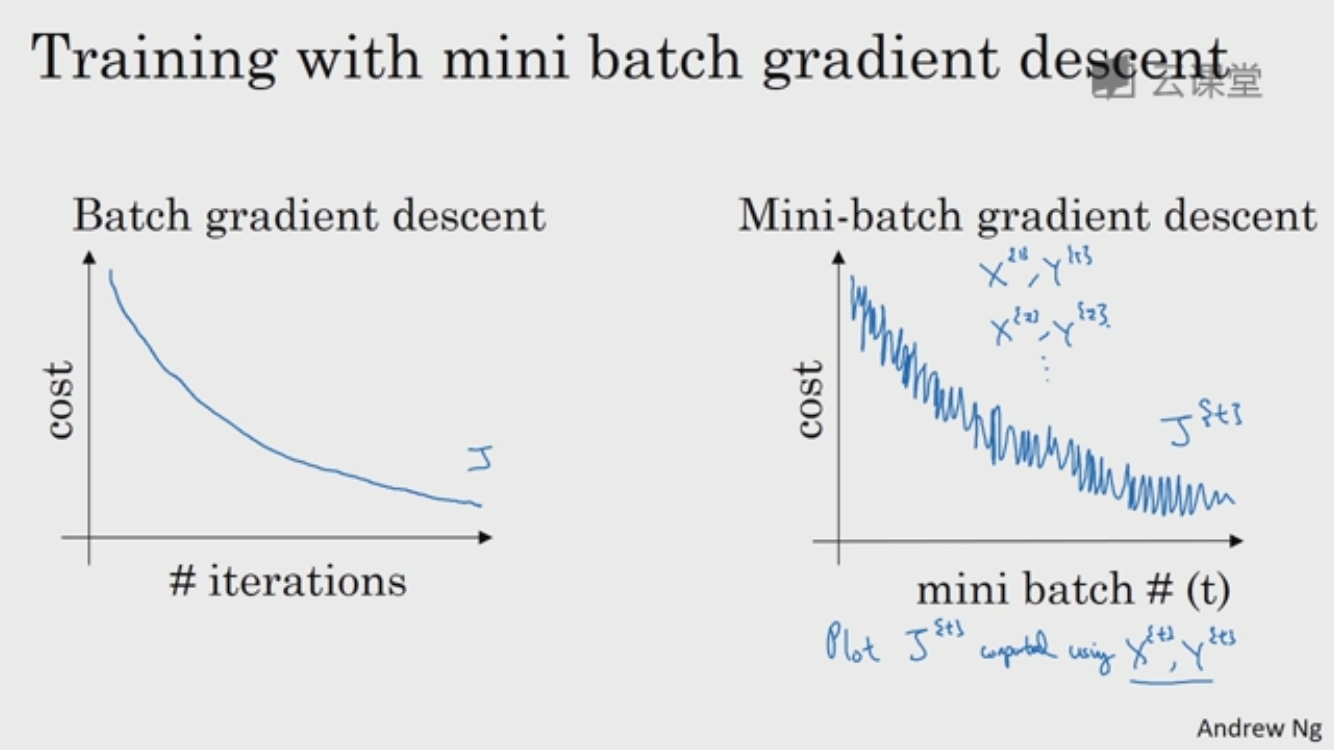
Mini-batch 梯度下降法比 batch 梯度下降运行更快,那么一个问题是 怎么选择 mini-batch size?
- size=m
Batch gradient descent(BGD)
每一次迭代都对 m 个样本进行计算,计算量大,耗时长 - size=1
如果 minibatch 的 size 为 1,就称为 随机梯度下降(stochastic gradient descent, SGD),每次迭代仅对一个样本计算梯度,随机梯度下降永远不会收敛,只会在最小值附近波动,但并不会达到并在最小值处停下,也就很容易陷入局部最优解
另外,每次处理一个样本,SGD 并没有利用 vectorization 的优势 - 1 < size < m
介于 BSD 和 SGD 之间,每次选取一定量的训练样本将进行迭代,速度比 BGD 快,比 SGD 慢,精度比 BGD 低,比 SGD 高
另外还有一种方法是 带 mini-batch 的 SGD,用来缓解 SGD 每次用一个样本容易陷入局部最优解的问题,过程是样本分为 mini-batch,然后在对每个 mini-batch 里计算单个样本的梯度然后求和取平均作为该 mini-batch 的梯度来更新参数。
最后还有一种 Online GD,应对线上实时的、有不间断的训练数据产生的应用。在线学习(Online Learning) 算法就是充分利用实时数据的一个训练算法。与 mini-batch GD/SGD的区别在于,所有训练数据只用一次,然后丢弃。这样做的好处是可以追踪模型的变化趋势。比如搜索广告的点击率(CTR)预估模型,网民的点击行为会随着时间改变。用batch算法(每天对所有历史数据重新训练更新模型),耗时长,也无法及时反馈用户的点击行为迁移。
Momentum
比标准的 gradient descent 要快,基本想法是,计算梯度的 指数加权平均数(exponentially weighted average of gradients),并利用该梯度更新权重。
直观上讲,希望横轴学习更快,纵轴学习更慢(不希望有那么剧烈的波动),Momentum 的过程如下:
On iteration t:
Compute dw, db on current mini-batch
$$
\begin{aligned}
v_{dw} &= \beta v_{dw}+(1-\beta)dw \\
v_{db} &= \beta v_{db}+(1-\beta)db \\
w &= w-\alpha v_{dw} \\
b &= b-\alpha v_{db} \\
\end{aligned}
$$
平均这些梯度,纵轴上的波动平均值接近于 0,平均过程中,正负抵消,纵轴方向摆动变小,而所有的的微分都指向横轴,横轴的平均值仍然很大,横轴方向运动更快,相当于走了更直接的路径。把代价函数想象成碗状函数,那么微分项提供了加速度,momentum v 像速度,$\beta$ 表现出摩擦性,所以球不会无限加速下去,原来的 gradient descent 每一步独立于上一步,而现在球可以从向下滚获得动量。
初始化的 $V_{dw}=0,V_{db}=0$,两个矩阵分别和 dw、db 有相同维数。也有做法会把 $1-\beta$ 去掉,这样的话其实 $\alpha$ 就需要根据 $1 \over 1-\beta$ 做相应变化,会影响到学习率 $\alpha$ 的最佳值。
最常见的 $\beta$ 是0.9,平均了前10次迭代的梯度,效果不错。
另外关于指数加权平均,各数值的加权而随时间而指数式递减,越近期的数据加权越重,这个过程实际上是一个递推的过程,不像普通求解平均值需要保留所有的数值然后求和除以n,这种方法只需要保留 n-1 时刻的平均值和 n 时刻的数值就好,这样可以减少内存和空间的做法。
优点是积累的速度v可以让我们越过局部最小点,但也可能造成在全局最优点来回震荡。
RMSprop
RMSprop 用的是 moving average of squared gradients,它会联系之前的每一次梯度变化情况来更新学习步长。如果当前得到的梯度为负,那学习步长就会减小一点点;如果当前得到的梯度为正,那学习步长就会增大一点点。
On iteration t:
Compute dw, db on current mini-batch
$$
\begin{aligned}
s_dw &= \beta s_dw + (1-\beta)s_dw^2 \ square, elementwise \\
s_db &= \beta s_db + (1-\beta)s_db^2 \\
w &= w-\alpha {dw \over \sqrt{s_{dw}+\epsilon}} \\
b &= b-\alpha {db \over \sqrt{s_{db}+\epsilon}} \\
\end{aligned}
$$
我们希望 $s_dw$ 相对很小,$s_db$ 相对很大,这样就可以减缓纵轴上的变化,就可以用更大的学习率。在实践过程中,分母不能为 0,所以要加上个很小的 $\epsilon$
Adam
Adam(Adaptive Moment Estimation),将 Momentum 和 RMSprop 结合到一起,并加入了 bias correction(指数加权平均刚开始计算时, $v_t$ 与 $\theta_t$ 偏差很大, bias correction 用于解决该问题),优点是在经过偏置校正后,每一次迭代学习率都有个确定范围,使得参数比较平稳。
$v_dw=0, s_db=0, v_db=0, s_db=0$
On iteration t:
Compute dw, db on current mini-batch
$$
\begin{aligned}
v_dw &= \beta_1 v_{dw} + (1-\beta_1)dw, \ \ v_db = \beta_1 v_{db} + (1-\beta_1)db \\
s_dw &= \beta s_{dw}+(1-\beta_2)dw^2, s_db = \beta s_{db}+(1-\beta_2)db^2 \\
v^{corrected}_{dw} &= {v_{dw} \over (1-\beta^t_1)}, \ \ v^{corrected}_{db}={v_{db} \over (1-\beta^t_1)} \\
s^{corrected}_{dw} &= {s_{dw} \over (1-\beta_2^t)}, \ \ s^{corrected}_{db}={s_{db} \over (1-\beta_2^t)} \\
w &= w - \alpha {v^{corrected}_{dw} \over \sqrt{s_{dw}+\epsilon}}, \ \ b = b - \alpha {v^{corrected}_{dw} \over \sqrt{s_{dw}+\epsilon}} \\
\end{aligned}
$$
$\beta_1: 0.9 $ -> dw
$\beta_2: 0.999$ -> $dw^2$
$\epsilon: 10^{-8}$
Learning rate decay
在学习初期,你能承受较大的步伐,但当开始收敛的时候,小的学习率能让你步伐小一点,下面列举了几种 decay 的方法,$\alpha$ 是初始学习率。
$$
\begin{aligned}
\alpha &= {1 \over 1 + decay-rate * epoch-num}\alpha_0 \\
\alpha &= 0.95^{epoch-num}\alpha_0 \\
\alpha &= {k \over \sqrt{epoch-num}}\alpha_0 \\
\alpha &= {k \over \sqrt t}\alpha_0 \\
\end{aligned}
$$
或者也可以使用离散下降的学习率,开始的 5000 step 用这个学习率,之后的 5000 step 把原来的学习率降低一半……
还有一种更朴实的,人工来控制学习率,像 babysitting 一样,不断观察着训练效果,人工来调整。

