主要介绍 基于用户的协同过滤算法(UserCF) 和 基于物品的协同过滤算法(ItemCF)。
基于邻域的算法是推荐系统中最基本的算法,主要分两大类,一类是基于用户的协同过滤算法,另一类是基于物品的协同过滤算法。协同过滤的本质其实是 KNN,我们要定义的是 什么是“最匹配”。下述的实验设计见 推荐系统–用户行为和实验设计
基于用户的协同过滤算法(User CF)
当一个用户 A 需要个性化推荐时,先找到和他有相似兴趣的其它用户,然后把那些用户喜欢的、而用户 A 没有听说过的物品推荐给 A。强调 把和你有相似爱好的其他的用户的物品推荐给你
过程:
- 将一个用户对所有物品的偏好作为一个向量来计算用户之间的相似度,找到和目标用户兴趣相似的用户集合;
- 找到这个集合中的用户喜欢的,且目标用户没有访问过的物品,计算得到一个排序的物品列表作为推荐。
算法与实验
用户-用户
计算用户之间的相似度。
Jaccard 公式
$$W_{uv}={|N(u) \cap N(v)| \over |N(u) \cup N(v)|}$$
- N(u): 用户 u 喜欢的物品集合
- N(v): 用户 v 喜欢的物品集合
余弦相似度
$$W_{uv}={|N(u) \cap N(v)| \over \sqrt{|N(u) || N(v)|}}$$
|
|
算法优化:
对两两用户都计算余弦相似度,时间复杂度是 O(|U|*|U|),在用户数很大的时候非常耗时。而很多用户相互之间并没有对同样的物品产生过行为,很多时候 $|N(u) \cap N(v)|=0$,有计算的浪费。所以可以换个思路,首先计算 $|N(u) \cap N(v)| \neq 0$ 的用户对 (u,v),然后再对这种情况除以分母 $\sqrt{|N(u) || N(v)|}$
具体做法:
- 建立物品到用户的倒排表
对于每个物品都保存对该物品产生过行为的用户列表
令稀疏矩阵 $C[u][v]=|N(u) \cap N(v)|$
E.g. 用户 u 和 v 同时属于倒排表中 K 个物品对应的用户列表,就有 $C[u][v]=K$ - 建立用户相似度矩阵
扫描倒排表中每个物品对应的用户列表
将用户列表中的两两用户对应的 $C[u][v]$ 加 1,得到所有用户之间不为 0 的 $C[u][v]$
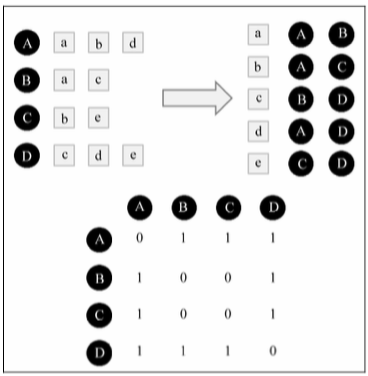
代码:
用户-物品
用户 u 对物品 i 的感兴趣程度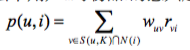
- S(u,K): 和用户 u 兴趣最接近的 K 个用户
- N(i): 对物品 i 有过行为的用户集合
- $w_{uv}$: 用户 u 和用户 v 的兴趣相似度
- $r_{uv}$: 用户 v 对物品 i 的兴趣,单一行为的隐反馈数据下,所有的 $r_{uv}=1$
代码
UserCF 实验
UserCF 只有一个重要的参数 K,即每个用户选出 K 个和他兴趣最相似的用户。
不同 K 值下 UserCF 算法的性能指标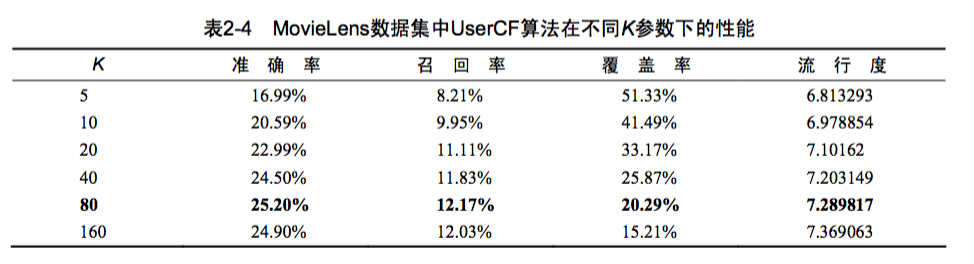
对比实验:
- Random 算法
每次随机挑选 10 个用户没有产生过行为的物品推荐给用户
准确率和召回率远高于 Random 算法,但覆盖率非常低,结果都非常热门 - MostPopular 算法
按照物品的流行度给用户推荐他没产生过行为的物品中最热门的 10 个物品
准确率和召回率很低,但覆盖率很高,结果平均流行度很低。

参数 K 的影响:
- 准确率和召回率
没有线性关系,在一定区域内都可以获得不错的精度 - 流行度
K 越大 UserCF 推荐结果越热门
K 越大参考的人越多,推荐结果就越趋近于全局热门的物品 - 覆盖率
K 越大,覆盖率越低
越趋近于推荐全局热门的物品,长尾物品的推荐越来越少
用户相似度优化
考虑 idf 类似影响,如果绝大多数人都买过《新华字典》,并不能说明他们兴趣相似,所以需要惩罚用户 u 和用户 v 共同兴趣列表中热门物品对他们相似度的影响,通过 ${1 \over log1+|N(i)|}$
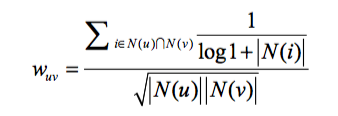
代码
UserCF-IIF 实验

发现 UserCF-IIF 在各项性能上略优于 UserCF。
小结
相比于 ItemCF,UserCF 在目前的实际应用中使用并不多。
优点和适用场景:
- 可以发现用户感兴趣的热门物品
- 用户有新行为,不一定造成推荐结果的立即变化
- 适用于用户较少的场合,否则用户相似度矩阵计算代价很大
- 适合时效性较强,用户个性化兴趣不太明显的领域
缺点:
- 数据稀疏性。一个大型的电子商务推荐系统一般有非常多的物品,用户可能买的其中不到1%的物品,不同用户之间买的物品重叠性较低,导致算法无法找到相似用户。
- 算法扩展性。随着用户数量越来越大,计算用户相似度矩阵越来越困难,时空复杂度的增长和用户数的增长近似于平方关系。
- 对新用户不友好,对新物品友好,因为用户相似度矩阵不能实时计算
- 很难提供令用户信服的推荐解释

基于物品的协同过滤算法(Item CF)
假设:物品 A 和物品 B 具有很大的相似度是因为喜欢物品 A 的用户大多也喜欢物品 B
通过分析用户的行为记录计算物品之间的相似度。强调 把和你喜欢的物品相似的物品推荐给你。在京东、天猫上看到「购买了该商品的用户也经常购买的其他商品」,就是主要基于 ItemCF。
过程:
- 基于用户对物品的偏好计算相似度,找到相似的物品;
- 根据物品的相似度和用户的历史行为预测当前用户还没有表示偏好的物品,计算得到一个排序的物品列表作为推荐。
过程:
- 计算物品之间的相似度
- 根据物品的相似度和用户的历史行为给用户生成推荐列表
算法与实验
物品-物品
Jaccard 公式:
$$W_{ij}={|N(i) \cap N(j)| \over |N(i)|}$$
- N(i): 喜欢物品 i 的用户数
- $|N(i) \cap N(j)|$: 喜欢物品 i 和物品 j 的用户数
同样的,考虑 idf 影响:如果物品 j 很热门,很多人都喜欢,那么 $W_{ij}$ 就会很大,接近 1,也就是说,任何物品会和热门的物品有很大相似度,所以惩罚物品 j 的权重,减轻热门物品和许多物品相似的可能性。
$$W_{ij}={|N(i) \cap N(j)| \over \sqrt{|N(i) || N(j)|}}$$
和 UserCF 类似,ItemCF 也可以首先建立用户-物品倒排表(每个用户建立一个包含他喜欢的物品的列表),然后对于每个用户,将他物品列表中的物品两两在共现矩阵 C 中加 1。
代码
左边是输入的用户记录,每一行代表一个用户感兴趣的物品集合,然后对每个物品集合,将里面对物品两两加一,得到一个矩阵。最终将这个矩阵相加得到 C 矩阵,其中 $C[i][j]$ 记录了同时喜欢物品 i 和物品 j 的用户数,最后,将 C 矩阵归一化可以得到物品之间的余弦相似度矩阵 W。
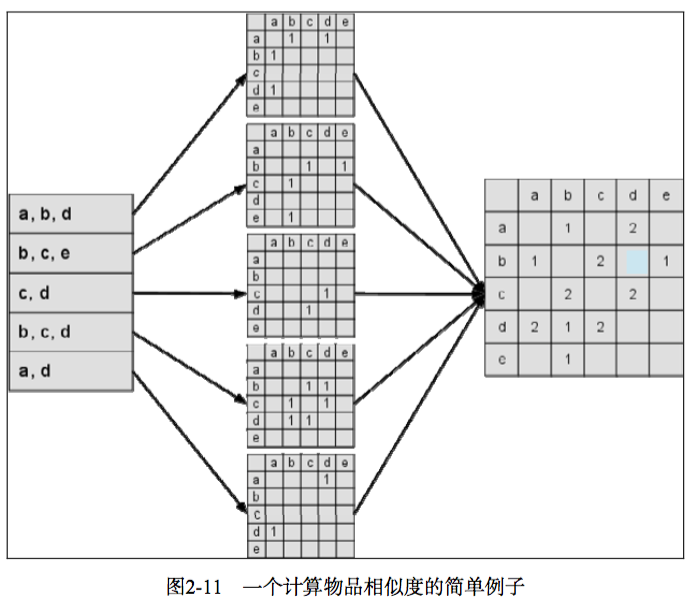
用户-物品
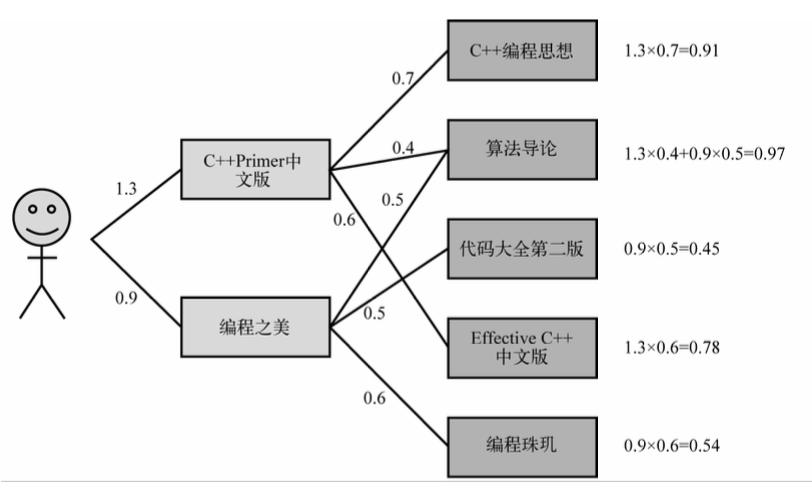
得到物品的相似度后,计算用户 u 对一个物品的兴趣: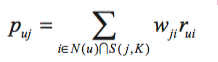
和用户历史上感兴趣的物品越相似的物品,越有可能在用户的推荐列表中获得比较高的排名。
- N(u): 用户喜欢的物品集合
- S(j,K): 和物品 j 最相似的 K 个物品的集合
- $w_{ji}$: 物品 j 和 i 的相似度
- $r_{ui}$: 用户 u 对物品 i 的兴趣
隐反馈数据集,如果用户 u 对物品 i 有过行为,即可令 $r_{ui}=1$
|
|
ItemCF 实验
不同 K 值下的性能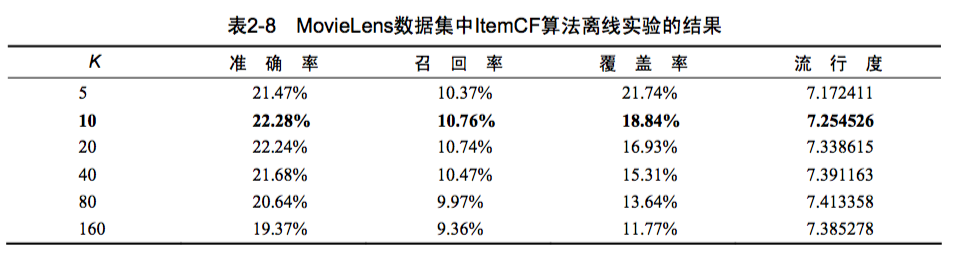
参数 K 的影响:
- 准确率和召回率
没有线性关系,在一定区域内都可以获得不错的精度 - 流行度
随着 K 的增加,流行度逐渐提高
当 K 增加到一定程度,流行度不再有明显变化 - 覆盖率
K 越大,覆盖率越低
用户活跃度对物品相似度的影响
举个例子吧,一个用户,是开书店的,买了亚马逊上 80% 的书准备用来自己卖,所以购物车里包含了亚马逊上 80% 的书,假设亚马逊一共有 100 万本书,那么这意味着 80 万本书两两之间产生了相似度,内存里将诞生一个 80w * 80w 的矩阵。
然而,虽然用户很活跃,但这些书并非基于兴趣,而且这些书覆盖了亚马逊图书的很多领域,所以这个用户对他所购买书对两两相似度的贡献应该远远小于一个只买了十几本自己喜欢的书的文学青年。
所以我们需要一个 IUF(Inverse User Frequency),来修正物品相似度的计算公式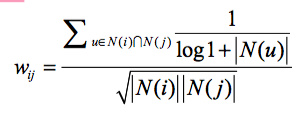
为了避免相似度矩阵过于稠密,我们在实际计算中一般直接忽略他的兴趣列表,而不将其纳入到相似度计算的数据集中。
可以看到,ItemCF-IUF 明显提高了覆盖率
物品相似度的归一化
将相似度矩阵按最大值归一化,可以提高推荐的准确率、覆盖率和多样性。对相似度矩阵 w 进行
$$w’_{ij}={w_{ij} \over max_j w_{ij}}$$
举个例子,假设有 A、B 两类物品,A 类物品之间的相似度是 0.5,B 类物品之间的相似度是 0.6,A 类物品和 B 类物品之间的相似度是 0.2,如果一个用户喜欢了 5 个 A 类物品和 5 个 B 类物品,ItemCF 推荐的是 B 类物品,而如果归一化之后,A 类物品的相似度和 B 类物品的相似度都是 1,那么推荐列表中 A 类物品和 B 类物品的数目也应该是大致相等的,这就保障了多样性。
归一化后的性能
小结
因为物品直接的相似性相对比较固定,所以可以预先在线下计算好不同物品之间的相似度,把结果存在表中,当推荐时进行查表,计算用户可能的打分值。
优点和适用场景:
- 可以发现用户潜在的但自己尚未发现的兴趣爱好
- 有效的进行长尾挖掘
- 利用用户的历史行为给用户做推荐解释,使用户比较信服
- 适用于物品数明显小于用户数的场合,否则物品相似度矩阵计算代价很大
- 适合长尾物品丰富,用户个性化需求强的领域
缺点:
- 对新用户友好,对新物品不友好,因为物品相似度矩阵不需要很强的实时性
UserCF vs ItemCF
总的而言,UserCF 的推荐更社会化,着重于反应和用户兴趣相似的小群体的热点,ItemCF 的推荐更个性化,着重于维系用户的历史兴趣。大家都觉得 Item CF 从性能和复杂度上比 User CF 更优,其中的一个主要原因就是对于一个在线网站,用户的数量往往大大超过物品的数量,同时物品的数据相对稳定,因此计算物品的相似度不但计算量较小,但这种情况只适应于提供商品的电子商务网站,对于新闻,博客或者微内容的推荐系统,情况往往是相反的,物品的数量是海量的,同时也是更新频繁的。一般来说,这两种算法经过优化后,最终得到的离线性能是近似的。具体选择还是要看具体情境。
社交网络/新闻领域
适用 UserCF:
- 用户兴趣不是特别细化
绝大多数都喜欢看热门的新闻,即使是个性化,也是比较粗粒度的,如体育/新闻这种大类。 - 个性化新闻推荐更加强调抓住新闻热点
热门程度和时效性是个性化推荐的重点,UserCF 可以给用户推荐和他有相似爱好的一群其他用户今天都在看的新闻,这样在抓住热点和时效性的同时,保证了一定程度的个性化。 - 物品的更新速度远远快于新用户的加入速度
在新闻网站中,物品的更新速度远远快于新用户的加入速度,而且对于新用户,完全可以给他推荐最热门的新闻。
ItemCF 需要维护一张物品相关度的表,如果物品更新很快,那么这种表也需要很快更新,这在技术上很难实现。
非社交网络
如图书/电商/电影网站,适用 ItemCF
- 用户的兴趣比较持久
- 用户不太需要流行度来辅助他们判断一个物品的好坏,而是可以通过自己熟悉领域的只是自己判断物品的质量
- 个性化推荐的任务是帮助用户发现和他研究领域相关的物品。
- 物品数目较少,物品相似度相对于用户的兴趣一般比较稳定。
- 提供推荐解释
对比

哈利波特问题
主要指某个物品太热门导致很多物品都与之相关。
解决方案:
- 分母上加大对热门物品的惩罚
$$W_{ij}={|N(i) \cap N(j)| \over |N(i)|^{1- \alpha} |N(j)|^{\alpha}}$$
$\alpha \in [0.5,1]$,通过提高 $\alpha$,就可以惩罚热门的 j。$\alpha$ 越大,覆盖率越高,结果的平均热门程度就越低,因此通过这种方法可以在适当牺牲准确率和召回率的情况下显著提升结果的覆盖率和新颖性(降低流行度即提高了新颖性)。
然而,这并不能彻底解决哈利波特问题。每个用户一般都会在不同的领域喜欢一种物品。两个不同领域的最热门物品之间往往具有比较高的相似度,这个时候,仅仅靠用户行为数据是不能解决这个问题的,因为用户的行为表示这种物品之间应该相似度很高。此时,我们只能依靠引入物品的内容数据解决这个问题,比如对不同领域的物品降低权重等,这些就不是协同过滤讨论的范畴了。

