CMU 11611 的课程笔记。主要是关于意义表示的一些理论性知识,重点掌握一阶谓词演算(First Order Predicate Calculus)
Semantics Road Map

- Lexical semantics
- Vector semantics
- Meaning representation languages and semantic roles
- Compositional semantics, semantic parsing
- Discourse and pragmatics
语义分析常用的知识源
- 词本身的意义
• Word-sense identifier, like bass7
• Morphological info
• Grammatical info (POS, etc.)
• Phonetic info, if speech system
• Semantic info
• Comments, etc. - 语法结构所带的意义
- 话语的结构知识
发生话语的上下文知识以及与话题相关的常识
这一篇讲 meaning representation,它常见的应用场景有:- 在考试中回答文章问题
具有背景知识,如关于问题主题的背景知识、关于学生知识水平的背景知识以及关于如何正常回答(answered normally)这些问题的背景知识 - 在饭店里阅读菜单点菜
阅读菜单、点什么菜、到哪里吃饭、根据菜谱做菜、编写新的菜谱等等这些都要求对食品有深入的知识,知道怎样做菜,知道人们喜欢吃什么以及喜欢到什么饭店等 - 通过阅读说明书学习使用新软件
要求对当前计算机、有关软件及使用有深入知识,对用户有一般知识
注意的是这一篇的重点是表示句子的字面意义(literal meaning),关注的是与单词的常规意义紧密联系的表示,而不反映它们出现的上下文环境,这种表示在涉及到俗语(idioms)和比喻(metaphor)时会显得不足。
Desirable qualities
探讨 Meaning representation 的最基本要求。
Verifiability
我们需要确定 meaning representation 的真实性,最直接的办法就是把 representation 和知识库(knowledge base)的表示相比较或匹配。
比如下面这个句子
|
|
假定这个问题包含了 Maharani serves vegetarian food 的意义,将其简单注释为 Serves(Maharani, VegetarianFood),那么我们就要看这个输入的 representation 是否能和关于饭店(restaurant)的事实知识库(knowledge base of facts)相匹配,返回结果如下
- If 在知识库中找到一个表示与之匹配 -> 返回一个肯定回答
- Elif 知识库是完全的 -> 返回否定
- Else -> 返回不知道
这个概念就是 可能性验证(verifiability),也就是系统把意义表示所描述的情况与在知识库中所模拟的某个世界的情况进行比较的一种能力。
Unambiguous Representation
无歧义表示(Unambiguous Representation) 要求最终的 meaning representation 只能有一个无歧义的表示,如下面的例子,我们只能准确的捕捉其中一种意义,而不能同时表示两种。有一些方法可以来决定某种解释比另外的解释更优先(或者更不优先),这一篇暂且不讨论这类技术。
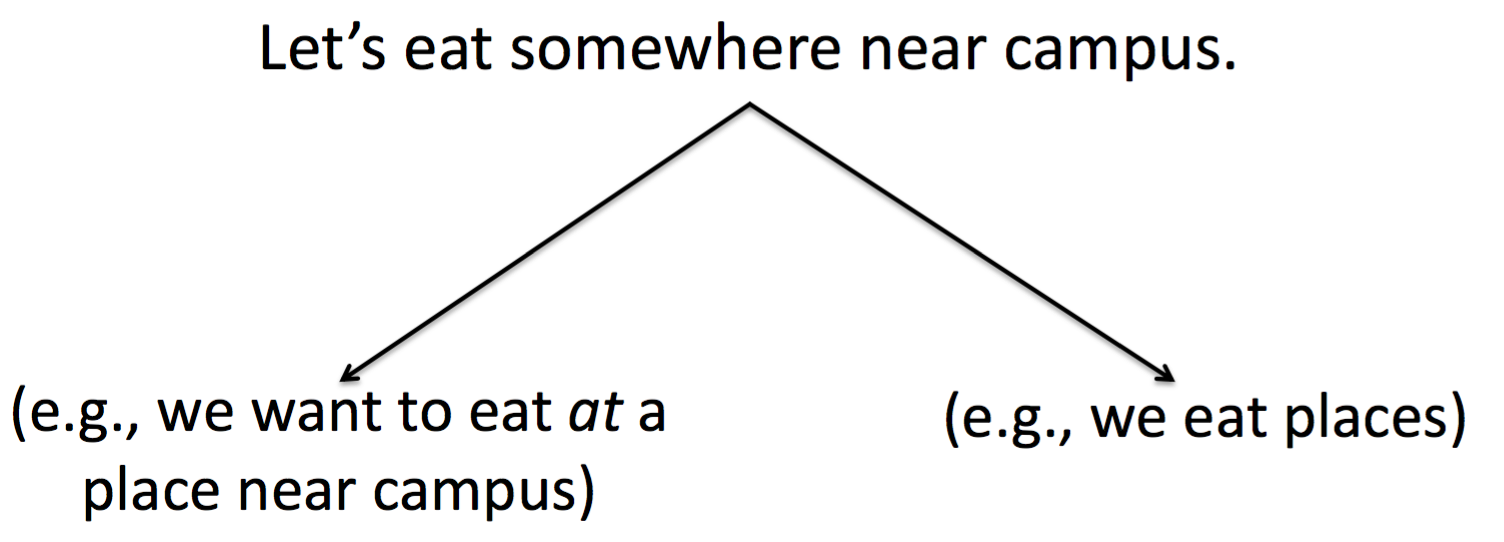
Canonical Form
规范形式(Canonical Form)要求的是表达相同事情的输入必须有相同的意义表示(input that mean the same thing should have the same meaning representation)。
比如下面四句话
|
|
系统必须把 vegetarian dishes, vegetarian food, vegetarian fare 归入在这种上下文环境中的同一个事物,同时,这里 have 和 serve 的用法也是等价的,我们希望 meaning representation 能做到这一点。有一种思路是,查下字典,会发现这些单词都具有许多不同词义(word sense),同时也可以看出,至少有一个意义是这些单词都共享的(可能是同义词synonymous),如果有能力从不同用法中筛选出这个共享的意义,就可以把同样的意义表示指派给不同的单词/短语。
Inference, Variables, and Expressiveness
推论(Inference)说明了系统根据输入的意义表示以及存储的背景知识做出可靠结论的能力。
看下面两个例子,对第一个问句而言,基于规范形式的方法和简单的匹配不能使系统对这个问题做出合适回答,我们需要把这个问题的意义表示和在知识库中表示的事实联系起来。
|
|
对于第二个句子而言,它并没有对任何特定的饭店进行推论,用户想要的是关于某个出售素食的饭店的信息,并没有提到特定的饭店,所以也不能进行简单匹配,需要引入 variable 来注释这句话,变成
$$Serves(x, VegetarianFood)$$
只有当 x 能够被知识库中某个已知的课题来替换,使整个命题得到匹配时,我们才可以说这个命题被成功匹配了,匹配完成后才可以用来实现用户的提问。
最后,意义表示方法应该具有足够的表达能力(expressiveness),最理想的情况当然是只用一个单独的意义表示语言(meaning representation language)就可以恰当表达任何自然语言的意义。当然这个期望可能太高了,下面会讲到一般的 一阶谓词演算(FOL)就具有足够的表达能力来处理多数问题。
Structure
下图说明了 I have a car 这个句子使用的四种常见的意义表示语言,第一行是 一阶谓词演算(First Order Predicate Calculus),中间部分是一个语义网络(Semantic Network),第三行包含一个概念依存(Conceptual Dependency)的图示和一个基于框架的表示(Frame-Based)
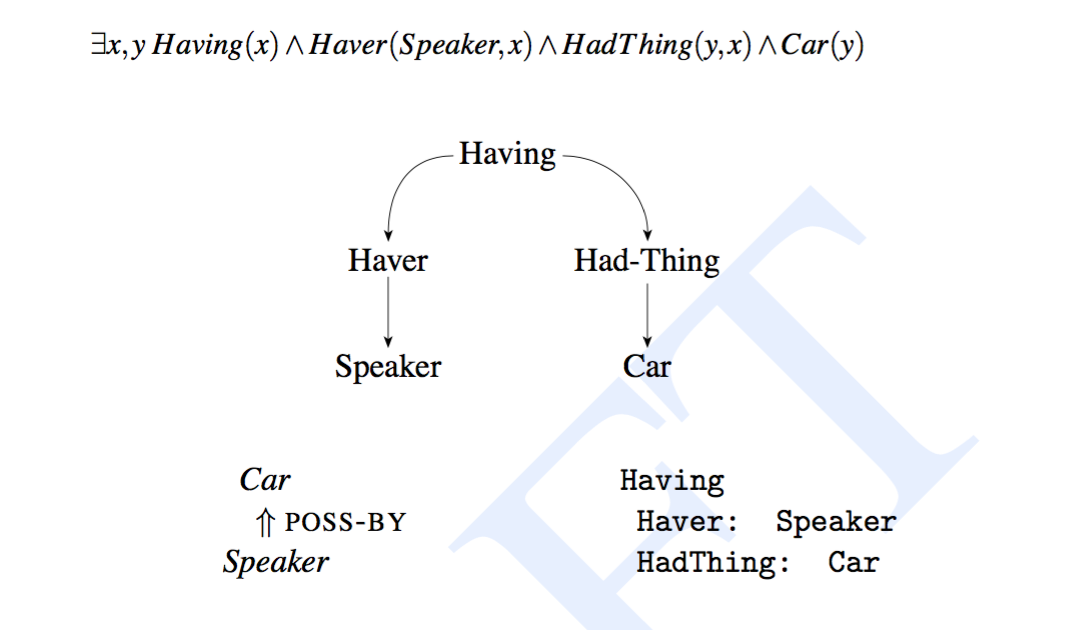
尽管四种方式各有差别,但是都表达了下面三个特征:
- 实体(Objects)
- e.g., people, restaurants, cuisines
- 实体性质(Properties of objects)
- e.g., pickiness, noisiness, spiciness
- 实体之间的关系(Relations between objects)
- e.g., serves(Oishii Bento, Japanese)
First Order Predicate Calculus
FOL(First Order Logic)可以用来表示 Objects, Relations, Functions
- Objects
Martin the cat - Relations
Martin and Moses are brothers - Functions
Martin’s age

上图是一个用于说明 EOPC 表示句法的一个上下文无关语法。逐个来看一下。
Term
先来看一下项(term)这个概念,项是 EOPC 表示客体的一种设置,包含三个信息块,常量(constant)、函数(function)和变量(variable),常量引用所描述的世界中的特定客体,函数在英语中经常表示为所属格(genitive)的概念,如 location of Maharani 或 Maharani’s location,翻译成 EOPC 可以表示为 LocationOf(Maharani),函数在局上上相当于一个单独的 argument predicate,但尽管外表上它很像 predicate,而实际上只涉及一个单独客体的“项”,这样的好处是,用函数来引用客体时,不用与命名它的常量相联系,当存在像饭店这样的很多命名客体时,如果使用函数,只需要像一个 location 这样的函数就可以与各种名字的饭店联系起来。变量之前提到过,就是方便我们对客体做出判断,进行推论,而不必参照任何特定命名客体。
Quantifier
另外,引用特定的匿名客体,以及一般性的引用在一个集合中的全部客体,都可以通过 量词(quantifier)来实现,存在量词(existential quantifier, ∃),读作 there exists,全称量词(universal quantifier, ∀),读作 for all。看一下解释
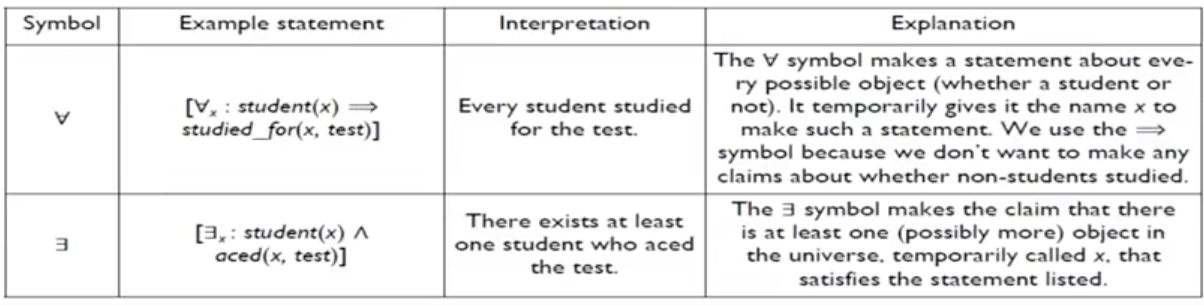
Predicates
再看一下 predicates,predicates 是一种符号,用于引用名称以及在给定领域内的一定数量的客体之间的关系,如
|
|
第一个表示的意思是,serve 是具有两个位置的 predicate,由常量 Maharani 和 VegetarianFood 标出的客体之间的关系,第二个表示略有不同,原句是 Maharani is a restaurant,predicate 只有一个位置,不涉及多个客体,只是确认一个单独客体的某个性质,这种情况下,predicate 对 Maharani 的范畴所属关系进行编码。
Connectives
Anyway,有了引用客体的能力(refer to objects)、确认关于客体事实的能力(assert facts about objects)、把一些客体与另外的客体相互联系的能力(relate objects to one another),就能够构造出初步的组合表示。而更大的组合表示需要逻辑连词(logical connective)把不同的意义表示结合到一起。如下
|
|
常用的连接词和解释
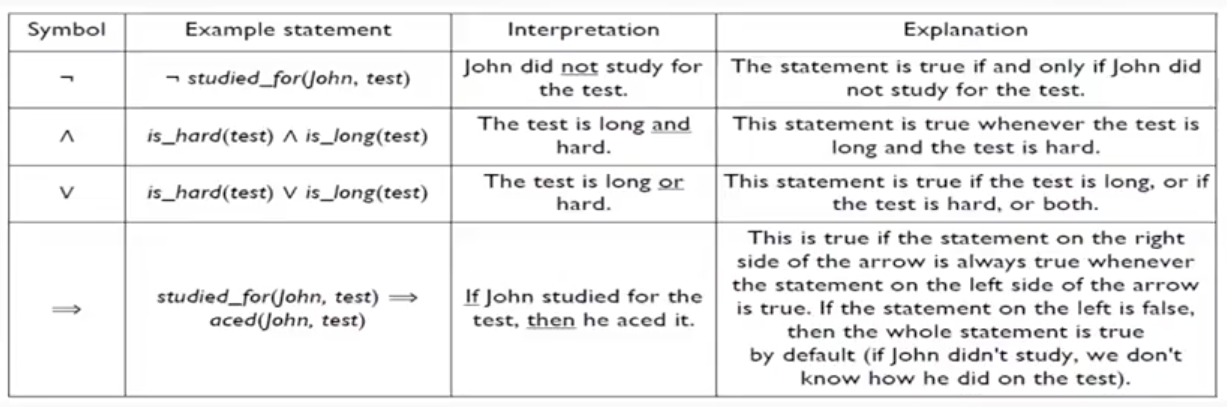
常见的两个错误:
=> 是 ∀ 的主要连词,∧ 和 ∀ 搭配往往会出错,如我们要表达 All cats eat fish,
123456Wrong:∀x Cat(x) ∧ EatsFish(x)Everyone is a cat and everyone eats fish.Correct:∀x Cat(x) => EatsFish(x)当然也有例外,如下面这句 ∧ 和 ∀ 搭配,就是对的
∀x Person(x) ∧ Know(I, x) => Smartness(x) < Smartness(Max)
Max is the smartest person I know.∧ 是 ∃ 的主要连词,=> 和 ∃ 搭配往往会出错,如我们要表达 There’s a cat that eats fish.
123456Wrong:∃x Cat(x) => EatsFish(x)is true if anyone who is not a cat (if leftside is False, then anything can go into right side)Correct:∃x Cat(x) ∧ EatsFish(x)
Example
具体来个例子,下面这个句子
|
|
通过辨认与句子中的各种语法成分对应的 term 和 predicate,并构造逻辑公式,可以得到下面的结果
|
|
这个公式的意义是根据 LocationOf(AyCaramba) 和 LocationOf(ICSI) 两项之间的关系、谓词 near 以及它们所模拟的世界中相应的客体和关系等而获得。这个句子可以根据在显示世界中 Ay Caramba 是不是真的和 ICSI 相近而被指派 True 或者 False 值。
两道题


第 1 题答案 DJBAE,第 2 题答案 ECDAH
Lambda Expression
lambda 符号(Church, 1940)提供了形式化参数的功能,对 FOPC 进行了扩充,它引入了下面的表达式:
$$\lambda x P(x)$$
$x$是变量,$P(x)$是使用这些变量的 FOPC 表达式。lambda表达式的意义在于可以生成新的 FOPC 表达式,在这些新的表达式中,形参变量由指定项来绑定,也就是 lambda 变量由指定的 FOPC 项来进行简单的字面替换,去掉 lambda,这个过程也就是 lambda 化简($\lambda$ -reduction),如下面将 lambda 表达式用于常量 A,对表达式进行化简
$$\lambda x P(x)(A)$$
$$P(A)$$
lambda符号提供了动词语义中需要的两种能力:形参表使我们获得变量集,lambda化简实现用项来替换变量的处理。
最简单的例子来理解:
if $inc(x) = \lambda x \ x+1$
then $inc(4) = (\lambda x \ x+1)(4)=5$
if $add(x,y) = \lambda x, \lambda y(x+y)$
then $add(3,4) = (\lambda x,\lambda y(x+y))(3)(4)=(\lambda y 3+y)(4)=3+4=7$
Semantics of FOL
FOL 句子可以被赋 true/false 值,如下
一些补充见 NLP 笔记 - Knowledge Representation
Inference
Modus Ponens
取式推理(Modus Ponens)相当于非形式化的 if-then 推理,比如说 $\alpha$ 和 $\beta$ 都是 EOPC 的公式,那么,可以把取式推理定义如下:

我们把 implication rule 的左边的项作为 前提(antecedent),右边的项作为 结论(consequent),如果前提在知识库中出现,那么就可以推论出结论。举个例子
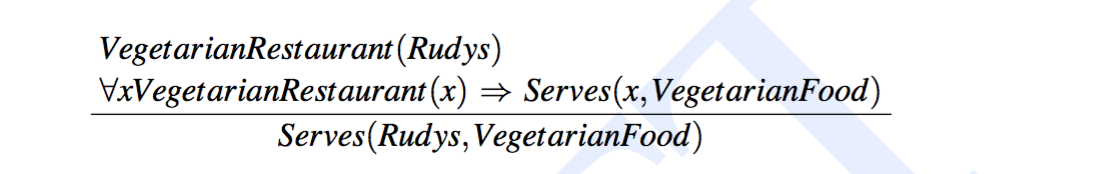
公式 VegetarianRestaurant(Rudys) 与前提相匹配,就可以用取式推理,得出 Serves(Rudys, VegetarianFood) 这个结论。
取式推理有两种应用方式,向前链接(Forward Chaining)和向后链接(Backward Chaining),向前链接就是刚才所描述的方法,优点是有关事实必须在知识库中表现出来,因为在向前链接中所有的推论都必须实现进行,这样可以充分减少回答下一个问题所需时间,因为这时只需要进行简单查询,而缺点是,所引用或存储的事实可能是以后永远都用不上的。产生式系统(production system)大量使用认知模型的研究成果,通过增加控制知识的方法来决定所要激发的规则,从而提升了向前链接系统。
Forward chaining as individual facts are added to the database, all derived inferences are generated
Backward chaining starts from queries, e.g., the Prolog programming language
关于向后链接(Backward Chaining),第一步是根据提问是否存储在知识库来判定提问公式是否为真,如果提问不在知识库中,下一步就搜索在知识库中有没有可以应用的 implication rule,如果一条规则的结果部分与提问公式相匹配,那么这条规则就是可应用的规则。如果存在任意这样的规则,并且规则的前提为真,那么提问就被证明了。然后把前提作为一个新的提问,就可以递归向后链接。还是以上面的例子为例,我们首先看 Serves(Rudys, VegetarianFood)在不在知识库中,发现它不在,就开始搜索一个可应用的规则可以让我们得到横线上面给定的规则。也就是用常量替换 x 后,证明 VegetarianRestaurant(Rudys)。Prolog就是一个向后链接的语言。如下面的例子,知识库中存在前 5 条知识,我们要证明最后一条 ?- father(M, bill) 是否为真,首先找到第一条,知道我们需要 parent(M, bill), male(M),才能证明 father(M, bill) 为真,然后发现,parent(john, bill) + male(john),即 M=john 时,father(M, bill) 为真,得证。
|
|
这里要注意的一个概念是向后链接(Backward Chaining) vs. 向后推理(Backward Inference)
- 向后链接是从提问到已知事实的推理
- 可靠的推理方法
- 向后推理是从已知结果到未知前提的推理
- 不可靠的推理方法
- 如果一个规则的结果为真,就假定其前提也为真
- 如果知道 Serves(Rudys, VegetarianFood) 为真,那么VegetarianRestaurant(Rudys)也为真
一些原则
Universal Instantiation
Existential Instantiation
Unification
Description Logics
除了 FOPC 外,常用的意义表示方法还有语义网络(Semantic network)、框架(frame)方法。其中框架方法又叫做槽填充(slot-filter)表示法,特征称为槽(slot),而这些槽的值用填充者(filter)来表示。这种表示方法比FOL的限制性更强。


