作为 NLP 笔记 - Meaning Representation Languages 这一篇的补充，简单介绍了事件(event)，时间(time)，信念(beliefs) 的意义表示。

Knowledge Representation

Ontologies
Mammal includes Cat,Dog,Whale
Cat includes PersianCat, ManxCat
Categories and Object
Categories: Cat; Object: Martin the cat
Categories is a set of object, object is part of categories
Events
Times
Beliefs

一些常见关系，ISA, AKO, HASA
ISA relation
is a ISA(Martin,Cat)
AKO relation
a kind of AKO(PersianCat,Cat)
HASA relation
has a HASA(Cat, tail)

Categories and Subsumption

范畴(Category)表示的是一种所属关系(ISA)，一个范畴的所有成员共享一套相关的特征，表示范畴的最普通方法是为每个范畴造出一个一元的谓词，这样的谓词可以对每个有关范畴进行说明。如

1 2	Maharani is an Indian restaurant. IndianRestaurant(Maharani)

左边的项是 category，括号里是 domain element。

Subsumption 表示的是一种包含关系(AKO)，如

1 2	All Indian restaurants are restaurants. IndianRestaurant ⊑ Restaurant

注意的是，IndianRestaurant(Maharani) 这种方法里范畴表示的是关系，而不是实实在在的客体，只能对构成关系的各个成分有所说明，而很难对于范畴本身有所说明，比如我们想表达

1	MostPopular(Maharani, VegetarianRestaurant)

这就不是一个合格的 FOPC 公式，因为 predicate 必须是 term，而不能是其他的 predicate。解决这个问题的方法是“具体化”(reification)，把我们想表述的所有概念都表示为实实在在的客体，这样就可以把 VegetarianRestaurant 这个范畴表示为诸如 Maharani 这样的客体啦，如

1 2	ISA(Maharani, IndianRestaurant) AKO(IndianRestaurant, Restaurant)

Representing Events

事件(event) 表示包括一个单独的谓词(predicate)以及与给定的例子想联系的角色所需的多个论元(argument)。以下面四个句子为例，动词 eat 这样的 predicate 的 argument 个数是可变的，然而这些例子都表示同一类事件

- Martin ate
- Martin ate in the morning
- Martin ate fish
- Martin ate fish in the morning

用 FOL 来表达，第一种方式是为动词所允许的每种 argument 格式建立一个次范畴化框架(subcategorization)，也就是为 eating 建立不同的谓词，来处理 eat 的各种可能的行为方式，这样就会比了 eating 究竟有多少个 argument 的问题，然而这种方法代价太高了

- Eating1(Martin)
- Eating2(Martin, Morning)
- Eating3(Martin, Fish)
- Eating4(Martin, Fish, Morning)

可以看到，事件之间在逻辑上存在着明显的关系，如如果 4 为真，3,2,1 也为真，然而这种方法并不能提供这些关系，一种解决方法是使用 意义假设(meaning postulate)，把谓词中的不同语义联系在一起

1
2
3

- ∀x,y,z Eating4(x,y,z) => Eating3(x,y)
- ∀x,y,z Eating4(x,y,z) => Eating2(x,z)
- ∀x,y,z Eating4(x,y,z) => Eating1(x)

很明显，这种方法负担太重，存在 scalability 的问题，也不适合处理个性化的事件。

第二种方式是只用一个框架来定义所有可能出现的 arguments，这种方法假定谓词的 argument 数目与该谓词在它的次范畴化框架中所表现出来的 argument 数目是相同的，然而在实际应用中，我们很难确定一个给定时间的正确角色数目

1 2	Eating4(x,y,z) with some arguments unspecified

造成的问题是

Too many commitments
Hard to combine Eating4(Martin, Fish, z) with Eating4(Martin,y,Morning)

第三种方式 Reification(具体化)，使事件成为能够量词化的客体，并且能够通过定义好的关系与其它客体联系起来，如

1	∃ e: ISA(e, Eating) ∧ Eater(e, Martin) ∧ Eaten(e,Fish)

表示存在一个吃饭的事件，Martin 是这个事件的行为者，Fish 是被吃的东西，这样的表示方法不需要说明量词的确定数目，无论出现多少角色和填充项都可以结合到谓词中，也不需要对角色进行意义假设。

Representing Time

很多句子包含了时间的信息，上面的语义表达并没有讨论时间表示的问题，这里介绍下时间表达的基本概念

- Martin went from the kitchen to the yard
- ISA(e,Going) ∧ Goer(e, Martin) ∧ Origin(e,kitchen) ∧ Target(e,yard)
Issue
- no tense information: past? present? future?
Fluents
- A predicate that is true at a given time: T(f,t)

我们可以增加时间变量事件的时间段(e.g., IntervalOf(w,i))、事件的终点(e.g., EndPoint(i,e))以及由动词时态(e.g., Precedes(e,Now))来说明关于这个终点到当前时间的时间谓词，然而简单动词的关系并不是直截了当的，现在时可以用于说明将来事件，将来时也可以用于说明一个过去事件，为了处理这种现象，Reichenbach(1947)提出了参照点(reference point)的概念，如下

E: event, R: reference, U: utterance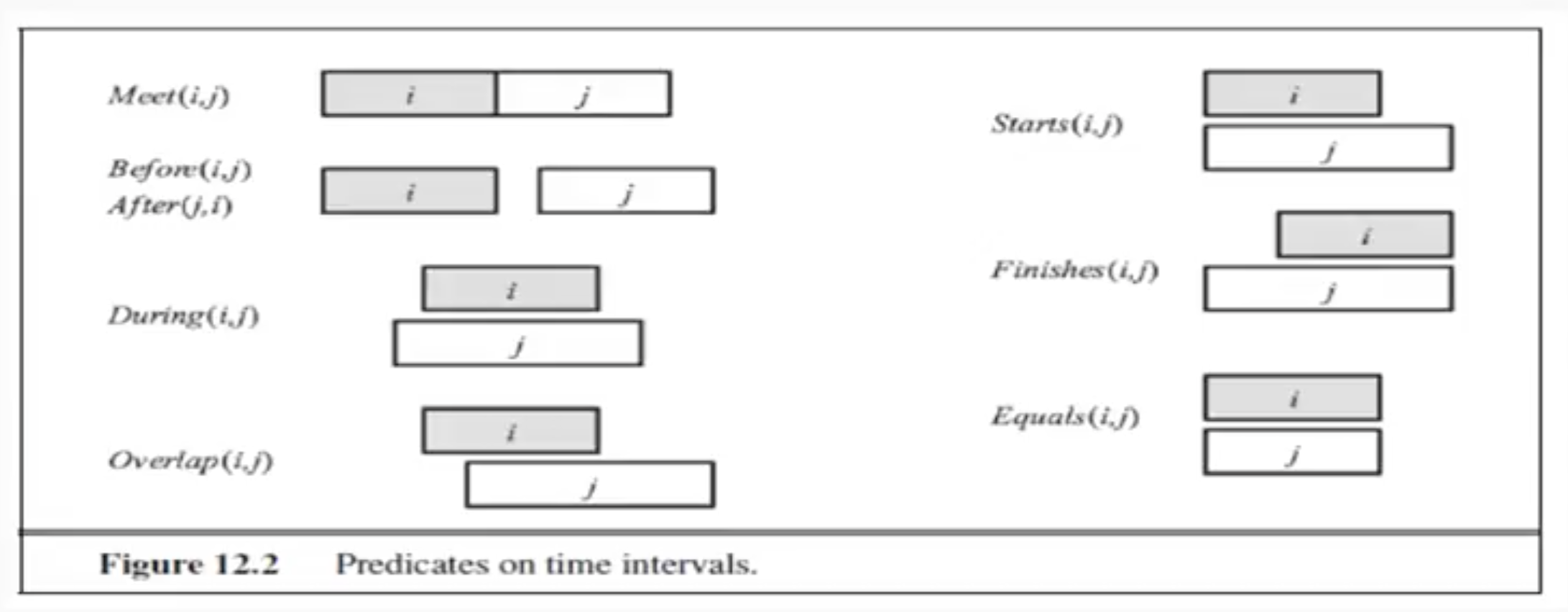

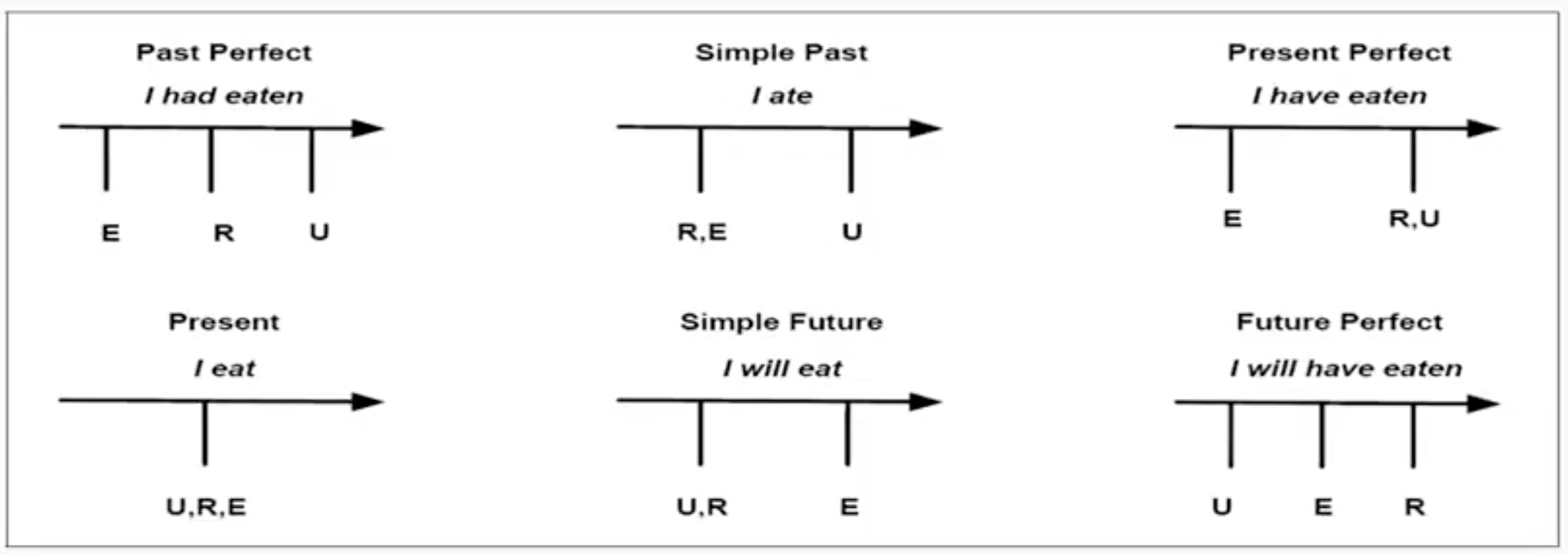
下面的例子中，departed 这个事件就是参照点(reference time)，吃饭事件在参照点之前

1	When Mary's flight departed, I had eaten lunch.

Representing Beliefs

有一些单词和词语的意义表示包含的逻辑公式并不一定在现实世界中真实存在，而是某个假设世界中的东西，这些单词具有“创造世界的能力”，如 believe, want, imagine, know 等。

Example
- Milo believes that Martin ate fish
One possible representation
- ∃ e,b: ISA(e,Eating) ∧ Eater(e,Martin) ∧ Eaten(e,Fish) ∧ ISA(b,Believing) ∧ Believer(b,Milo) ∧ Believed(b,e)

然而这种表示中，所有的连接部分都必须为真，这导致的结果是 “Martin ate fish”，漏掉了信念这个事件，然而，Speaker 的信念并不能使这个命题在现实世界中成为真命题。处理这种情况的标准方法是使用 operator 来增强 FOPC，我们可以引入一个称为 Believes 的 operator，取两个 FOPC 公式作为它的 argument，一个公式指派一个 believer，另一个公式指派所相信的命题，如

1	Believes(Milo, ∃ e: ISA(e,Eating) ∧ Eater(e,Martin) ∧ Eaten(e,Fish))

Believes 这样的 operator 又称为 模态算符(modal operator)，相应地，用 modal operator 来增强的逻辑，称为 模态逻辑(modal logic)

Other concepts

TBox and ABox

TBox包含了应用领域关于类别或概念的知识，如

1 2	All bistros are restaurants All restaurants are businesses

ABox包含了领域里关于个体的事实，如

1	India Garden is an Indian restaurant

Negation and Disjunciton

Negation

1 2	IndianRestaurant ⊑ not ItalianRestaurant Indian restaurants can’t also be Italian restaurants.

Disjunciton

1 2	Restaurant ⊑ (or ItalianRestaurant IndianRestaurant MexicanRestaurant) Restaurants are Italian restaurants, Indian restaurants, or Mexican restaurant.