系统总结下之前零零散散提到过的 smoothing 方法。

引入

我们来看一个概率模型，也就是 p(e)在 event space E 下的概率分布，模型很可能会用最大似然估计(MLE)，如下
$$P_{MLE}={c(x) \over \sum_ec(e)}$$

然而，由于并没有足够的数据，很多事件 x 并没有在训练数据中出现，也就是 c(x)=0，$P_{MLE}=0$，这是有问题的，没有在训练数据中出现的数据，并不代表不会在测试数据中出现，如果没有考虑到数据稀疏性，你的模型就太简单了！

Data sparsity 是 smoothing 的最大原因。Chen & Goodman 在1998 年提到过，几乎所有数据稀疏的场景下，smoothing 都可以帮助提高 performance，而数据稀疏性几乎是所有统计模型(statistical modeling)都会遇到的问题。而如果你有足够多的训练数据，所有的 parameters 都可以在没有 smoothing 的情况下被准确的估计，那么你总是可以扩展模型，如原来是 bigram，没有数据稀疏，完全可以扩展到 trigram 来提高 performance，如果还没有出现稀疏，就再往高层推，当 parameters 越来越多的时候，数据稀疏再次成为了问题，这时候，用合适的平滑方法可以得到更准确的模型。实际上，无论有多少的数据，平滑几乎总是可以以很小的代价来提高 performance。

平滑方法

Additive smoothing
Good-Turing estimate
Jelinek-Mercer smoothing (interpolation)
Katz smoothing (backoff)
Witten-Bell smoothing
Absolute discounting
Kneser-Ney smoothing

差值(Interpolation) vs. 回退(backoff)

先来理解下平滑方法的两种思想，一个是差值，简单来讲，就是把不同阶的模型结合起来，另一种是回退，直观的理解，就是说如果没有 3gram，就用 bigram，如果没有 bigram，就用 unigram，两者的区别：

插值（Jelinek-Mercer）和回退（Katz）都涉及到来自较高和较低阶模型的信息
主要区别：在决定非零计数的 n-gram 的概率时，差值模型使用低阶模型的信息，而回退模型则不使用
相同点：在决定没有出现过的(零计数) n-gram 时，两者都用了低阶模型的信息
事实证明，做差值模型的回退版本和做回退模型的差值版本都不难~(Kneser-Ney最开始是回退模型，而 Chen&Goodman 也做了差值版本)

另外还有一点，与差值平滑算法相比，回退算法所需参数较少，而且可以直接确定，无需通过某种迭代重估算法反复训练，因此实现更加方便。

Additive smoothing

Add-one smoothing

也叫 Laplace smoothing，假设 we saw each word one more time than we did，下面以 bigram model 为例给出加 1 平滑的模型
MLE estimate:
$$P_{MLE}(w_i|w_{i-1})={c(w_{i-1}w_i) \over c(w_{i-1})}$$
Add-1 estimate:
$$P_{Add-1}(w_i|w_{i-1})={c(w_{i-1}w_i)+1 \over c(w_{i-1})+V}$$

通常情况下，V={w:c(w)$\gt$0}$\cup${UNK}

举个例子，假设语料库为下面三个句子

1
2
3

JOHN READ MOBY DICK
MARY READ A DIFFERENT BOOK
SHE READ A BOOK BY CHER

那么 JOHN READ A BOOK 这个句子的概率是：

而 CHEN READ A BOOK 这个句子出现的概率是：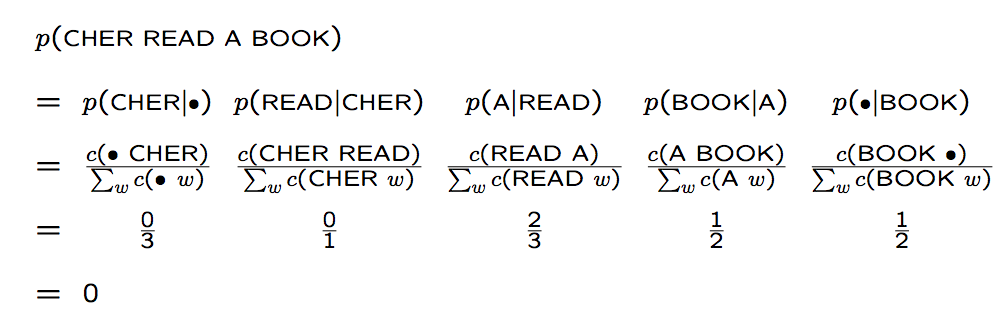

如果使用加1平滑，那么概率就变成了：

加 1 平滑通常情况下是一种很糟糕的算法，与其他平滑方法相比显得非常差，然而我们可以把加 1 平滑用在其他任务中，如文本分类，或者非零计数没那么多的情况下。

Additive smoothing

对加 1 平滑的改进就是把 1 改成 $\delta$，且 $0 \lt \delta \le 1$，也就是 pretend we’ve seen each n-gram $\delta$ times more than we have，当然，Gale & Church(1994) 吐槽了这种方法，说表现很差。

$$P_{Add-1}(w_i|w_{i-1})={c(w_{i-1}w_i)+\delta \over c(w_{i-1})+\delta V}$$

Good-Turing smoothing

基本思想: 用观察计数较高的 N-gram 数量来重新估计概率量大小，并把它指派给那些具有零计数或较低计数的 N-gram

Idea: reallocate the probability mass of n-grams that occur r+1 times in the training data to the n-grams that occur r times.

一般情况下，我们选出现过一次的概率，也就是 Things seen once 这一概念：
Things seen once: 使用刚才已经看过一次的事物的数量来帮助估计从来没有见过的事物的数量。举个例子，假设你在钓鱼，然后抓到了 18 条鱼，种类如下：10 carp, 3 perch, 2 whitefish, 1 trout, 1 salmon, 1 eel，那么
下一条鱼是 trout 的概率是多少？
很简单，我们认为是 1/18

那么，下一条鱼是新品种的概率是多少？
不考虑其他，那么概率是 0，然而根据 Things seen once 来估计新事物，概率是 3/18

在此基础上，下一条鱼是 trout 的概率是多少？
肯定就小于 1/18，那么怎么估计呢？
在 Good Turing 下，对每一个计数 r，我们做一个调整，变为 r*，公式如下，其中 $n_r$ 表示出现过 r 次的 n-gram。
$$r^* = (r+1){n_{r+1} \over n_r}$$

然后，我们就有
$$P_{GT}(x:c(x)=r) = {r^* \over N}$$

所以，c=1时，
$C^* (trout)= 2*1/3 = 2/3$
$P^* (trout)={2/3 \over 18}={1 \over 27}$

问题

然后，问题来了，如果 $n_{r+1}=0$ 怎么办？这在 r 很高的情况下很常见，因为在对计数进行计数时(counts of counts)，会出现 “holes”。即使没有这个 hole，对很高的 r 来说，$n^r$ 也是有噪音的(noisy)。

所以，我们应该这样来看 $r^*$:
$$r^* = (r+1){E(n_{r+1}) \over E(n_r)}$$

但是，问题是怎么估计这种期望呢？这需要更多的解释。

Jelinek-Mercer smoothing(Interpolation, 差值)

同样，以语言模型为例，我们看这样一种情况，如果 c(BURNISH THE) 和 c(BURNISH THOU) 都是 0，那么在前面的平滑方法 additive smoothing 和 Good-Turing 里，p(THE|BURNISH)=p(THOU|BURNISH)，而这个概率我们直观上来看是错误的，因为 THE 要比 THOU 常见的多，$p(THE|BURNISH)\gt p(THOU|BURNISH)$ 应该是大概率事件。要实现这个，我们就希望把 bigram 和 unigram 结合起来，interpolate 就是这样一种方法。

用线性差值把不同阶的 N-gram 结合起来，这里结合了 trigram，bigram 和 unigram。用 lambda 进行加权
$$
\begin{aligned}
p(w_n|w_{n-1}w_{n-2}) & = \lambda_1 p(w_n|w_{n-1}w_{n-2}) \\
& + \lambda_2 p(w_n|w_{n-1}) \\
& + \lambda_3 p(w_n)
\end{aligned}
$$

$$\sum_i \lambda_i=1$$

怎样设置 lambdas?
把语料库分为 training data, held-out data, test data 三部分，然后

Fix the N-gram probabilities(on the training data)
Search for lambdas that give the largest probabilities to held-out set:
$logP(w_1…w_n|M(\lambda_1…\lambda_k))=\sum_ilogP_M(\lambda_1…\lambda_k)(w_i|w_{i-1})$

这种差值其实是一个递归的形式，我们可以把每个 lambda 看成上下文的函数，如果对于一个特定的 bigram 有特定的计数，假定 trigram 的计数是基于 bigram 的，那么这样的办法将更可靠，因此，可以使 trigram 的 lambda 值更高，给 trigram 更高权重。

$$
\begin{aligned}
p(w_n|w_{n-1}w_{n-2}) & = \lambda_1 (w^{n-1}_{n-2})p(w_n|w_{n-1}w_{n-2}) \\
& + \lambda_2 (w^{n-1}_{n-2})p(w_n|w_{n-1}) \\
& + \lambda_3 (w^{n-1}_{n-2})p(w_n)
\end{aligned}
$$

通常 $\lambda w^{n-1}_{n-2}$ 是用 EM 算法，在 held-out data 上训练得到(held-out interpolation) 或者在 cross-validation 下训练得到(deleted interpolation)。$\lambda w^{n-1}_{n-2}$ 的值依赖于上下文，高频的上下文通常会有高的 lambdas。

Katz smoothing

回退式算法。和 Good-Turing 一样，对计数进行调整，以 bigram 为例，非 0 计数的 bigram 都根据打折比率 $d_r$ 进行打折，比率约为 ${r^* \over r}$，这个比率是由 Good-Turing 计算得到的，然后根据下一个低阶分布(如 unigram)，对没有出现过的 bigram 重新分配从非零计数中减去的值。

以 bigram 为例看看它是怎么做的：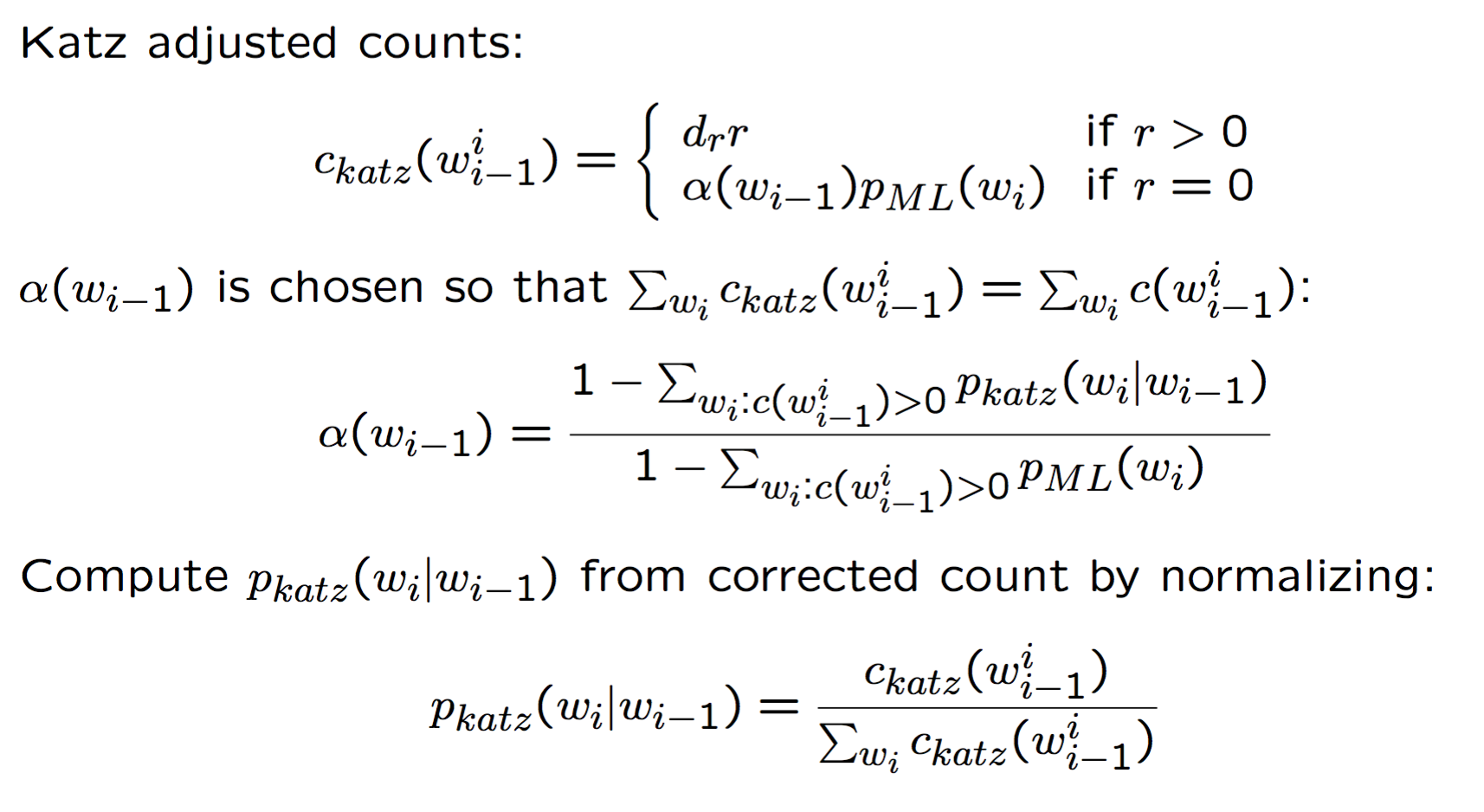

对于 $d_r$ 的一些探讨，当一个 n-gram 出现次数足够大时，MLE 其实是一个可靠的概率估计，而当计数不是足够大时，就可以采用 Good-Turing 对其进行平滑，让计数为 0 时，退回低阶模型。

Witten-Bell smoothing

一个 JM smoothing 的实例，当 n-gram $w^i_{i-n+1}$ 在训练数据中出现的时候，我们应该用高阶模型，否则，用低阶模型。所以 $1-w^i_{i-n+1}$ 应该是一个单词在训练数据中没有出现在 $w^i_{i-n+1}$ 后面的概率，可以用跟在 $w^i_{i-n+1}$ 后的 unique words 的数量来估计，公式为：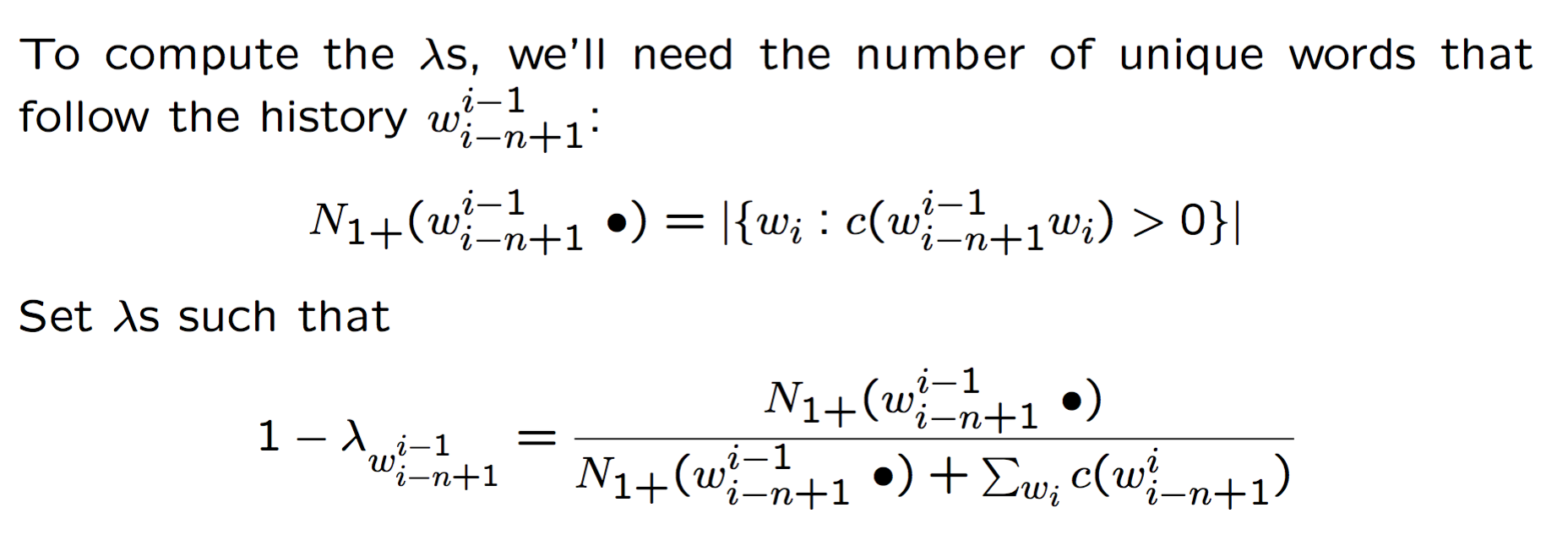

举个例子来理解一下，考虑 spite 和 constant 的 bigram，在 Europarl corpus 中，两个 bigram 都出现了 993 次，以 spite 开始的 bigram 只有 9 种，大多数情况下 spite 后面跟着 of(979次)，因为 in spite of 是常见的表达，而跟在 constant 后的单词有 415 种，所以，我们更有可能见到一个跟在 constant 后面的 bigram，Witten-Bell 平滑就考虑了这种单词预测的多样性，所以：

$1-\lambda_{spite}={9 \over 9+993}=0.00898$
$1-\lambda_{constant}={415 \over 415+993}=0.29474$

Absolute discounting

和 Jelinek-Mercer 相似，Absolute discounting 包括了对高阶和低阶模型的差值，然而它并不是用高阶模型的 $P_{ML}$ 乘以一个 lambda，而是从每个非零计数里减掉一个固定的 discount $\delta \in [0,1]$

先简单的来看下 bigram model，加上 Absolute discounting 就是：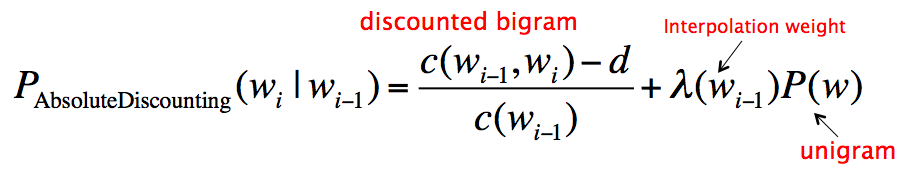

完整的公式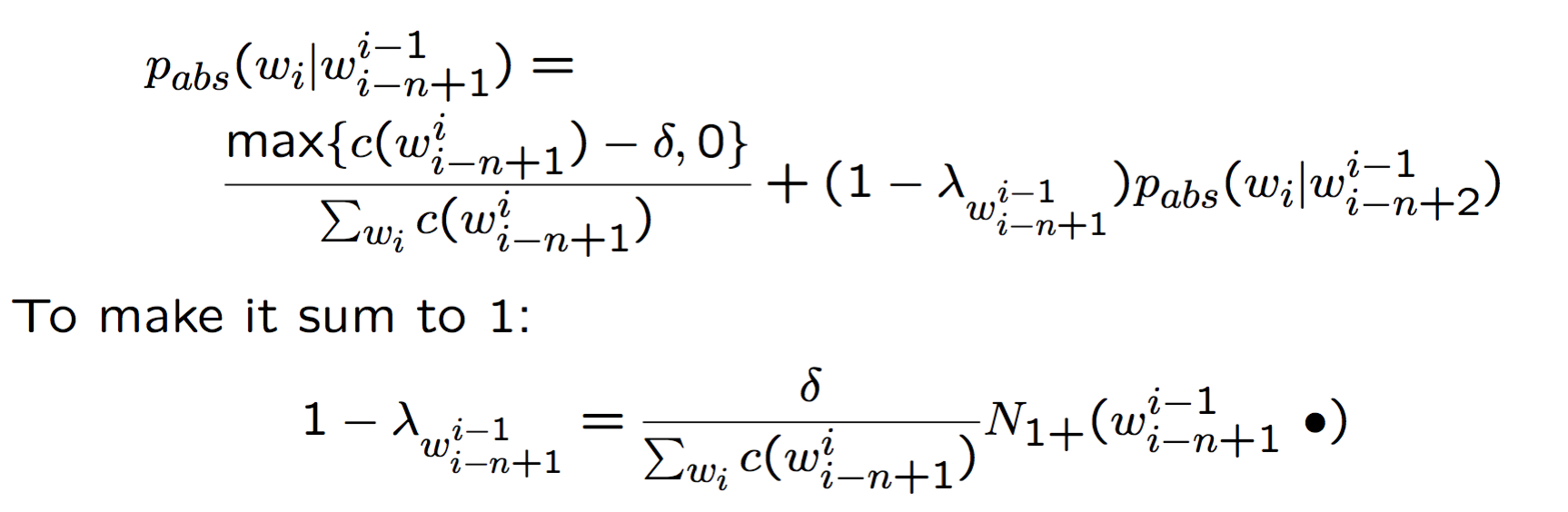

一般来说，$\delta$ 就直接取 0.75 好啦~

Kneser-Ney smoothing

是 Absolute discounting 的一个扩展，对回退部分做了一个修正。

Idea: 只有在高阶模型的计数很小或者为 0 时，低阶模型才显得重要，(换种说法，只有在 bigram 没有出现过时，unigram 才有用)，因此应针对该目的进行优化

举个例子

1	Shannon game: I can't see without my reading (Francisco/glasses)?

reading 后面跟 Francisco 还是 glasses 呢？因为 “San Francisco” 是个很常见的地名，所以 Francisco 有一个很高的 unigram 概率，比 glasses 高，而 Francisco 偏偏只在 San 后面出现，这就非常不合理。而更合理的方式是，给 Francisco 一个较低的 unigram 概率，这样，bigram 模型表现会更好。

改进的方案是，我们不看 how likely is w，而去看 how likely is w to appear as a novel continuation，也就是，对每个单词，我们看它对应的 bigram type 的数量，然后，每个 bigram type 在第一次出现的时候都是 novel continuation

所以最后的公式为: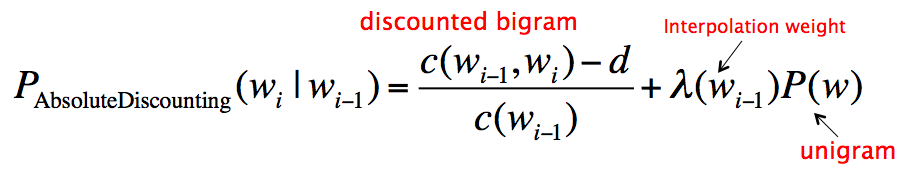

小结

影响最大的因素是使用 modified backoff distribution，如 Kneser-Ney smoothing
Jelinek-Mercer 平滑在小型训练数据集上表现更好，而 Katz 在大型训练集上表现更好
Katz 在计数大的 n-grams 上效果很好，而 Kneser-Ney 适合小的计数
Absolute discounting 要优于 linear discounting
在非零计数较低的情况下，Interpolated models 优于 backoff
添加 free parameters 到算法中，通过 held-out data 上优化这些参数可以提高性能

参考链接
Stanford Language Modeling
NLP Lunch Tutorial: Smoothing
Language models