之前有过一篇总结,词向量总结笔记(简洁版),这一次,从 intuition 角度来谈词向量的发展,对上一篇是一个补充。
大纲:
Distributional (vector) models of meaning
- Sparse:
PPMI-weighted word-word co-occurrence matrices - Dense:
Word-word SVD 50-2000 dimensions
Skip-grams and CBOW
Brown clusters 5-20 binary dimensions
Thesaurus-based meaning
之前谈到单词的相似度,可能会用到词典(thesaurus)。然而并不是每一种语言都有词典,我们也很难每年去更新词典,再者,基于词典的方法的召回率(recall)很低,很多单词和短语被漏掉了,而且词典在动词、形容词上的表现并不是很好。
Joint distributions model of meaning
用 joint distribution 来表示一个词?几乎不可能。英语大概有 1 百万的词,如果我们只考虑 unigram model,那么我们也得有 1 百万个参数,如果考虑 bigram,那么,至少有 10^12 的参数,想要稳定的估计,还必须要非常大的样本量,不管是获取还是处理这样的大的样本,都不容易。
Distributional models of meaning
所以有了新的方法,distributional models of meaning,它的 intuition 是词类的分布特征,如果两个单词能够出现在相似的环境中,它们往往是相似的,换句话说,就是 一个词是由它周围的单词来定义的,所以我们要得到的是当前词和它的周围词共同出现的次数。当然,这种方法并不能区分近义词反义词,如 fast 和 slow 在这种情况下就可能是同义的。
Distributional models of meaning = vector-space models of meaning = vector semantics
有几种不同类型的向量模型(vecotr models)
- Sparse vector representations
Mutual-information weighted word co-occurrence matrices - Dense vector representations:
Singular value decomposition (and Latent Semantic Analysis)
Neural-network-inspired models (skip-grams, CBOW)
Brown clusters
Sparse vectors
Words and co-occurrence vectors
先来看两个矩阵,词-文档矩阵(Term-document matrix) 和 词共现矩阵(Term-term matrix)
Term-document matrix
表示每个单词在文档中出现的次数(词频),每一行是一个 term,每一列是一个 document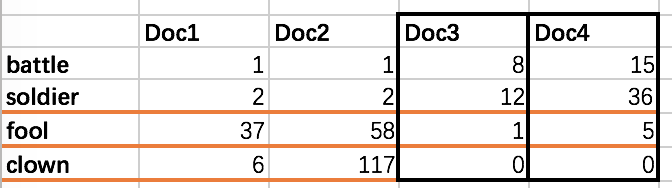
两篇文档的向量相似 => 两篇文档相似,如上图 doc3 和 doc4,我们就认为它们是相似的。
两个单词的向量相似 => 两个单词相似,如上图的 fool 和 clown,就是相似的。
Term-term matrix
然后我们可以考虑更小的粒度,更小的上下文,也就是不用整篇文档,而是用段落(paragraph),或者小的窗口(window of $\pm 4$ words),所以这个时候,向量就是对上下文单词的计数,大小不再是文档长度 |D|,而是窗口长度 |V| 了,所以现在 word-word matrix 是 |V|*|V|
看一个上下文为 7 个单词的 word-word matrix,同样,每一行是一个 term,每一列是一个上下文(context)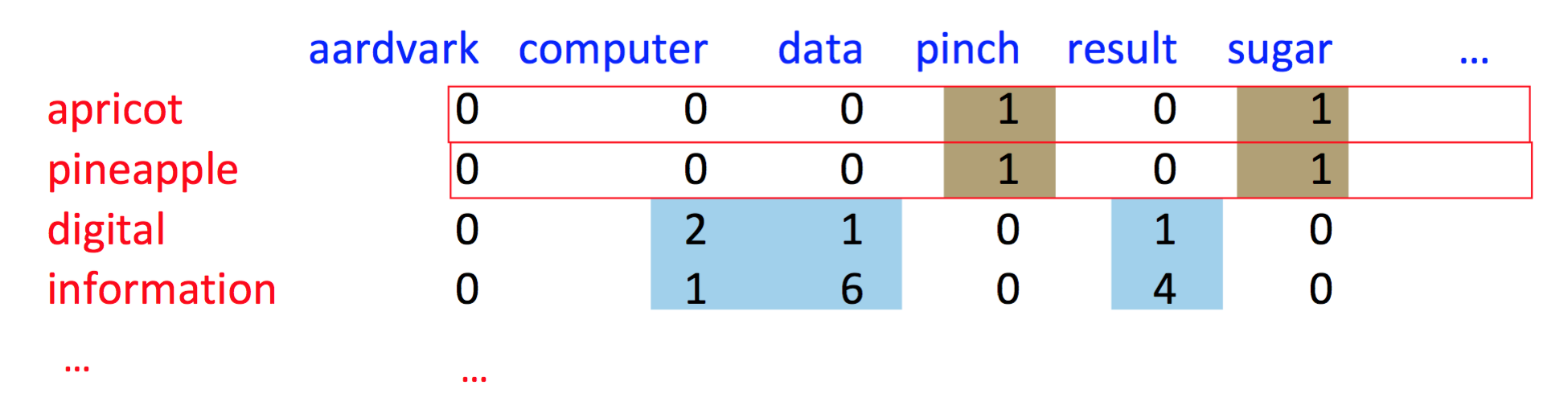
关于窗口的大小,还有一个基本知识,如果窗口很小,比如说在 $\pm$ 1-3 之间,那么这个向量是更加基于语法(syntactic)的向量,而如果窗口更长一些,比如说在 $\pm$ 4-10 之间,那么向量是更加基于语义(semantic)的。
实际情况下,这个矩阵依然是非常稀疏的,大多数值都是 0,然而这并没有什么问题,我们还是可以用很多高效的算法来处理这种稀疏矩阵。
Positive Pointwise Mutual Information(PPMI)
先来看看两种词共现(co-occurrence)的类型。
- First-order co-occurrence(syntagmatic association)
通常是临近词,比如说,wrote 是 book 或者 poem 的 first-order associate - Second-order co-occurrence(paradigmatic association)
通常有相似的临近词/上下文,比如说,wrote 是 said 或者 remarked 的 second-order associate
原始的词频对单词间的联系可能不是一个很好的估计,因为它非常的 skewed,一些停顿词如 the, of 非常的常见,也就没有区分度,而我们想要的是看 context word 能不能对 target word 提供有用的信息,于是就有了 PPMI。
先看下 PMI,看两个事件 x,y 同时出现的概率是不是比单独出现的概率高呢?
$$PMI(X,Y)=log_2{P(x,y) \over P(x)P(y))}$$
PMI 的范围是负无穷到正无穷,但是负值会带来各种各样的问题,所以我们通常会把负的 PMI 替换成 0,也就是有了 Positive PMI(PPMI)
$$PPMI(word_1,word_2)=max(log_2{P(word1,word2) \over P(word1)P(word2)},0)$$
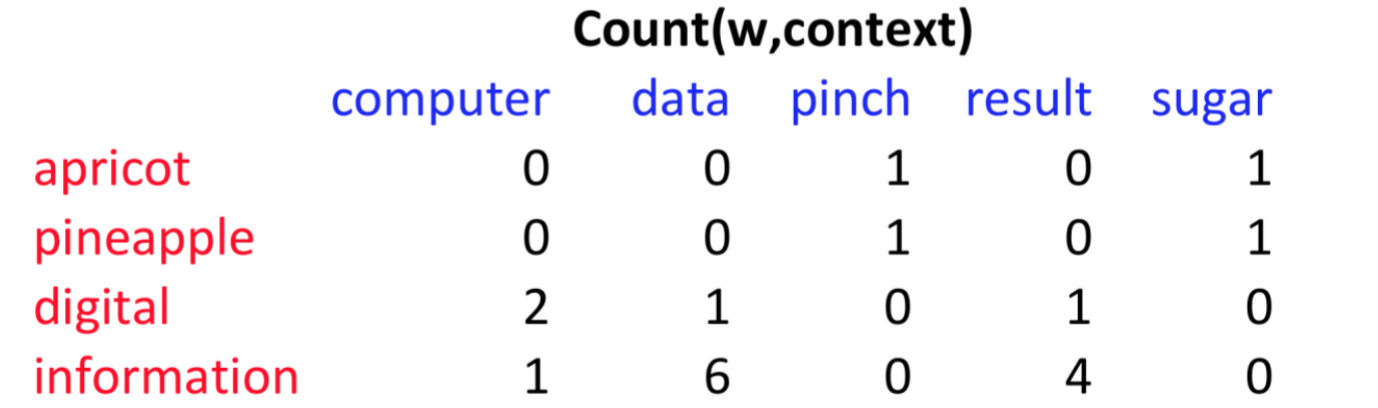
P(w=information, c=data)=6/19=.32
P(w=information)=11/19=.58
P(c=data)=7/19=.37
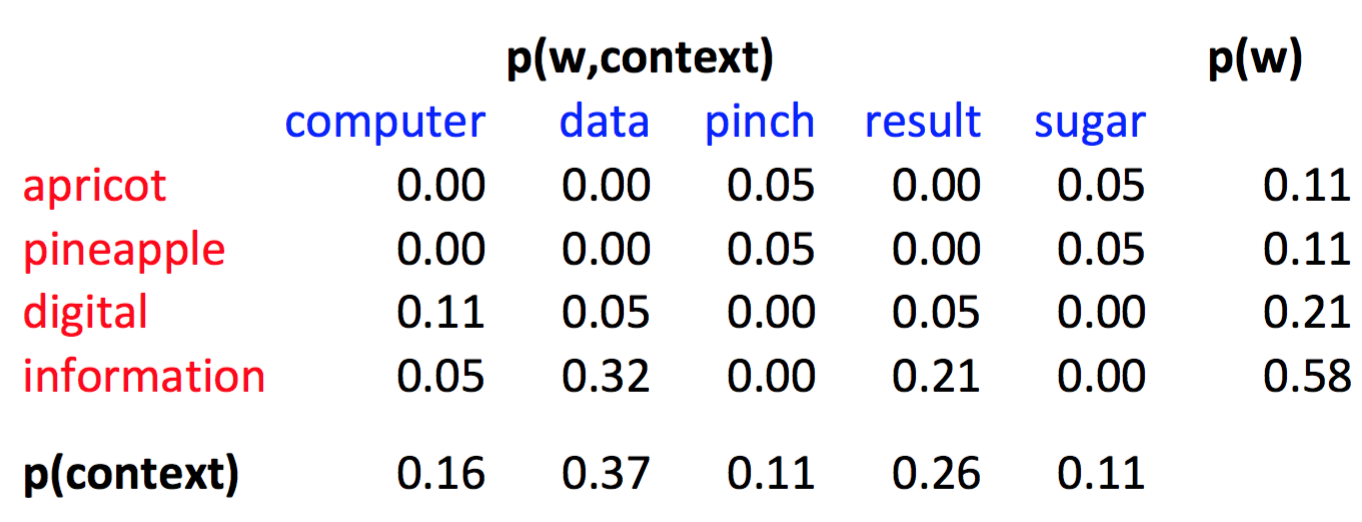
所以
$PMI(information,data)=log_2(.32 / (.37 * .58))=.57$
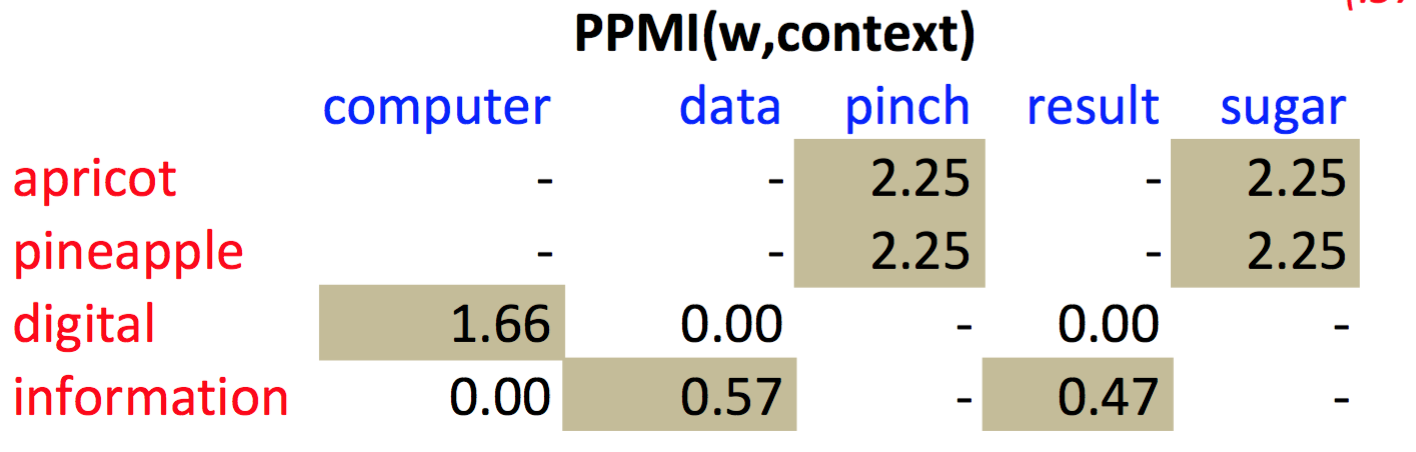
PMI 有 bias,rare words 会有很高的 PMI 值,有两个解决办法
- Give rare words slightly higher probabilites
- Add-one smoothing
Weighting PPMI
这也就是第一种解决办法,加上一个 $\alpha$,比如 $\alpha=0.75$
$$PPMI\alpha (w,c)=max(log_2{P(w,c) \over P(w)P\alpha (c)},0)$$
$$P\alpha (c)={count(c)^\alpha \over \sum_c count(c)^\alpha}$$
对罕见的 c 来说,$P\alpha(c) >> P(c)$,来个例子,P(a)=.99, P(b)=.01,那么 $P\alpha(a)={.99^.75 \over .99^.75 + .01^.75}=.97$,同理,$P\alpha(b)=.03$。
Add-k smoothing
前面讲过很多次 Add-k smoothing 啦,就不多说了,直接上图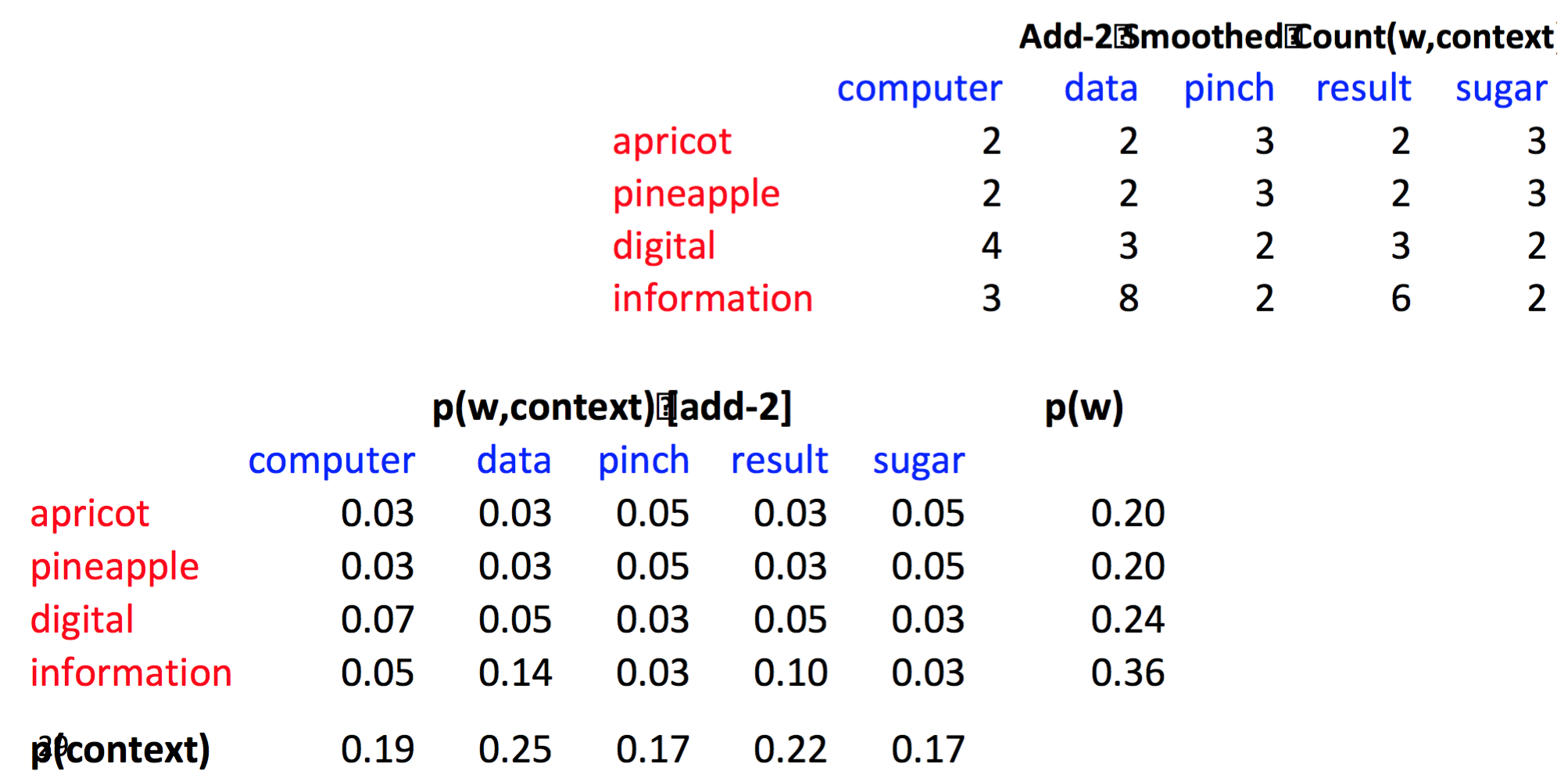
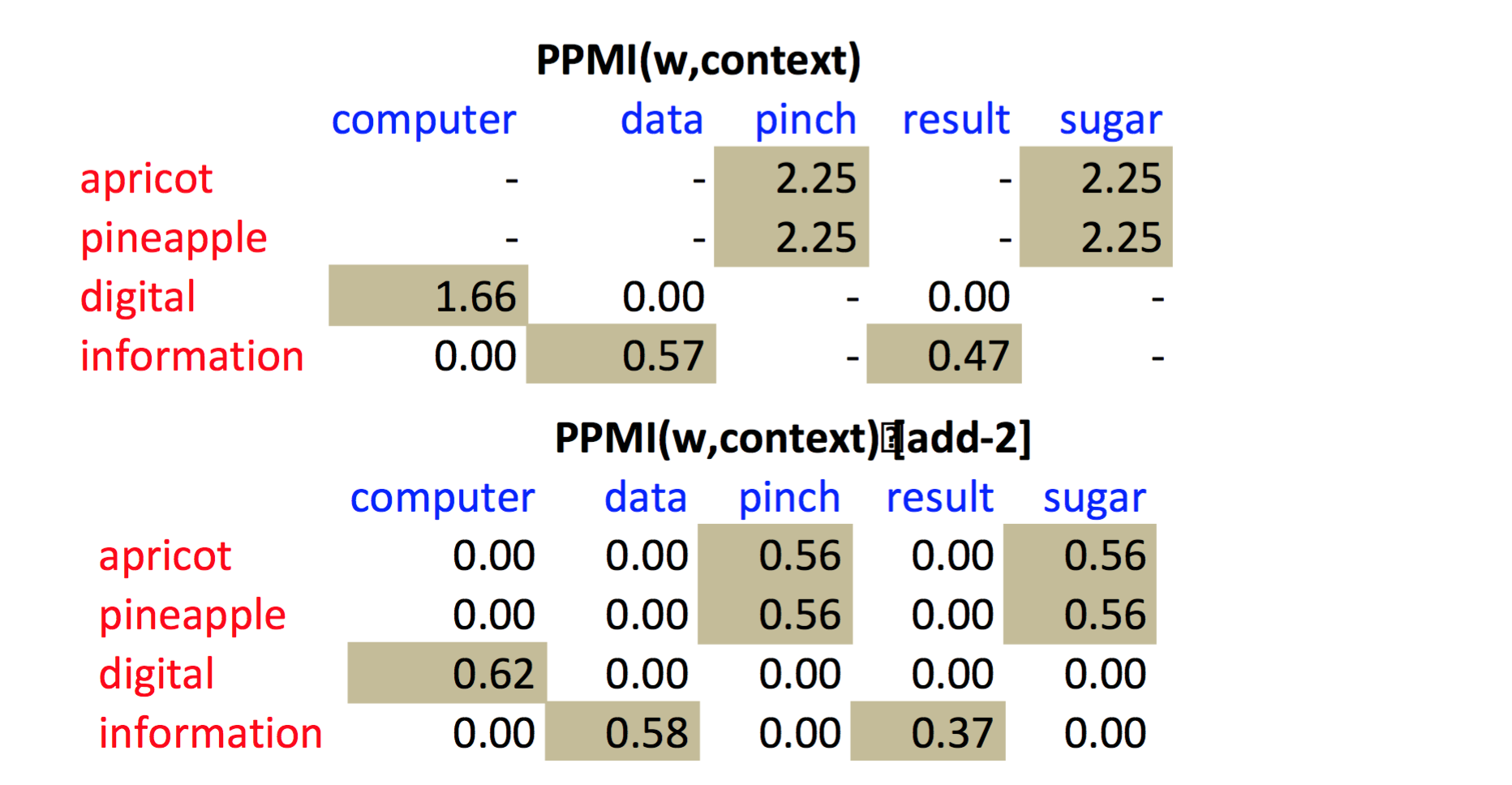
Measuring similarity: the cosine
cosine 就没啥好多讲的了,+1 就是相同方向,-1 就是相反方向,0 就是正交,垂直方向,因为 PPMI 不会是负的,也就是 cosine 的范围是 0-1,很简单,就不举例了,看一下其他的相似性度量方法。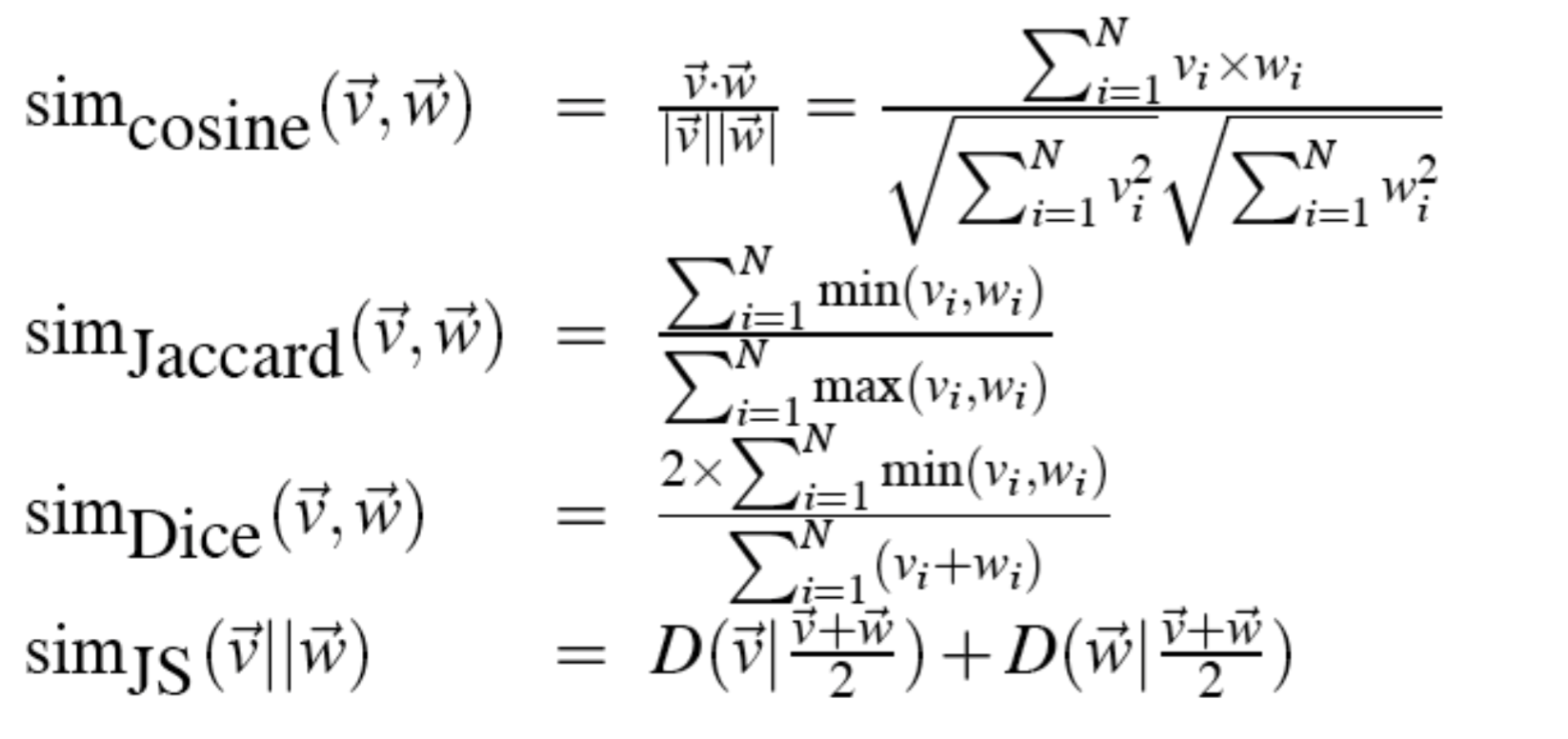
Adding syntax
加入句法特征,如果两个单词有相似的句法结构上下文,那么这两个单词就是相似的,比如说 duty 和 responsibility,看一下句法分布
- Modified by adjectives:
additional, administrative, assumed, collective, congressional, constitutional… - Objects of verbs:
assert, assign, assume, attend to, avoid, become, breach..。
Co-occurrence vectors based on syntactic dependencies
每个维度:在 R 个语法关系集合中的一个 context word,比如说 Subject-of-“absorb”
所以一个向量不是 |V| 个特征,而是 R|V| 个特征,举个例子,看一下 cell 这个单词的计数

注意这里的矩阵其实是 |V|*R|V| 大小的,也可以把它变成 |V|*|V| 大小的,举个例子
$$M(“cell”,”absorb”) = count(subj(cell,absorb)) + count(obj(cell,absorb)) + count(pobj(cell,absorb))$$
PMI 在依存关系的应用,看下面的例子,drink it 比 drink wine 更常见,然而 wine 比 it 更加 drinkable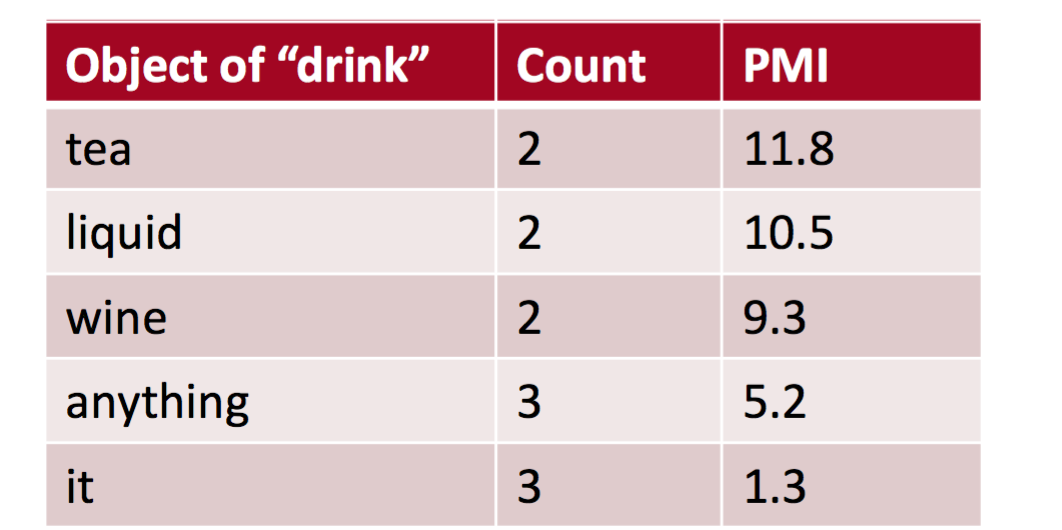
tf-idf
tfidf 是另一种替代 PPMI 来衡量关联性(association)的方法,通常来说,并不是从来计算单词与单词之间的相似度,而是来考虑单词与文档之间的联系。
Dense Vectors
PPMI 的向量很长(length |V|= 20,000 to 50,000),而且很稀疏(大多数元素都是 0),与之相对应的是稠密向量(dense vectors),它更加短(length 200-1000),更加稠密(大多数元素不是 0),稠密向量的好处在于,它更容易作为机器学习中的特征,因为需要更少的 weights,而另一方面,它更容易泛化,也能更好的捕获同义词。
怎样用更少的维度来估计 N 维的数据集?有很多相关方法
- PCA – principle components analysis
- Factor Analysis
- SVD
SVD
奇异值分解和特征值分解的目的都是提取一个矩阵最重要的特征,特征值分解要求变换的矩阵必须是方阵,而奇异值分解是一个能适用于任意矩阵的一种分解的方法。$A=U \Sigma V^T$,$\Sigma$ 除了对角线,其余元素都是 0,对角线元素就是奇异值,U 和 V 都是方阵,里面的向量分别是左奇异向量和右奇异向量,如下:
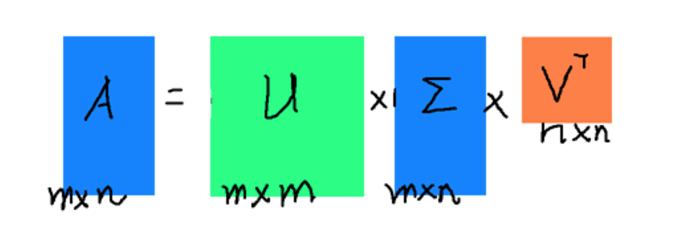
把奇异值和特征值对应起来,首先,我们将一个矩阵 A 的转置再乘以 A,将会得到一个方阵,我们用这个方阵求特征值可以得到 $(A^T A)v_i=\lambda_iv_i$,得到的 v 就是右奇异向量,然后还可以得到
$$\sigma_i = \sqrt {\lambda_i}$$
$$u_i={1 \over \sigma_i}Av_i$$
里面的 $\sigma$ 就是奇异值,u 就是左奇异向量。奇异值 σ 跟特征值类似,在矩阵 Σ 中也是从大到小排列,而且σ 减少特别的快,在很多情况下,前 10% 甚至 1% 的奇异值的和就占了全部的奇异值之和的 99% 以上了。也就是说,我们也可以用前 r 大的奇异值来近似描述矩阵,这里定义一下部分奇异值分解:
$$A_{m*n} \approx U_{m*r} \Sigma_{r*r}V^T_{r*n}$$
右边的三个矩阵相乘的结果将会是一个接近于 A 的矩阵,在这儿,r 越接近于 n,则相乘的结果越接近于 A。而这三个矩阵的面积之和(在存储观点来说,矩阵面积越小,存储量就越小)要远远小于原始的矩阵 A,我们如果想要压缩空间来表示原矩阵 A,我们存下这里的三个矩阵:U、Σ、V就好了。
看一下奇异值分解在词向量中的应用,
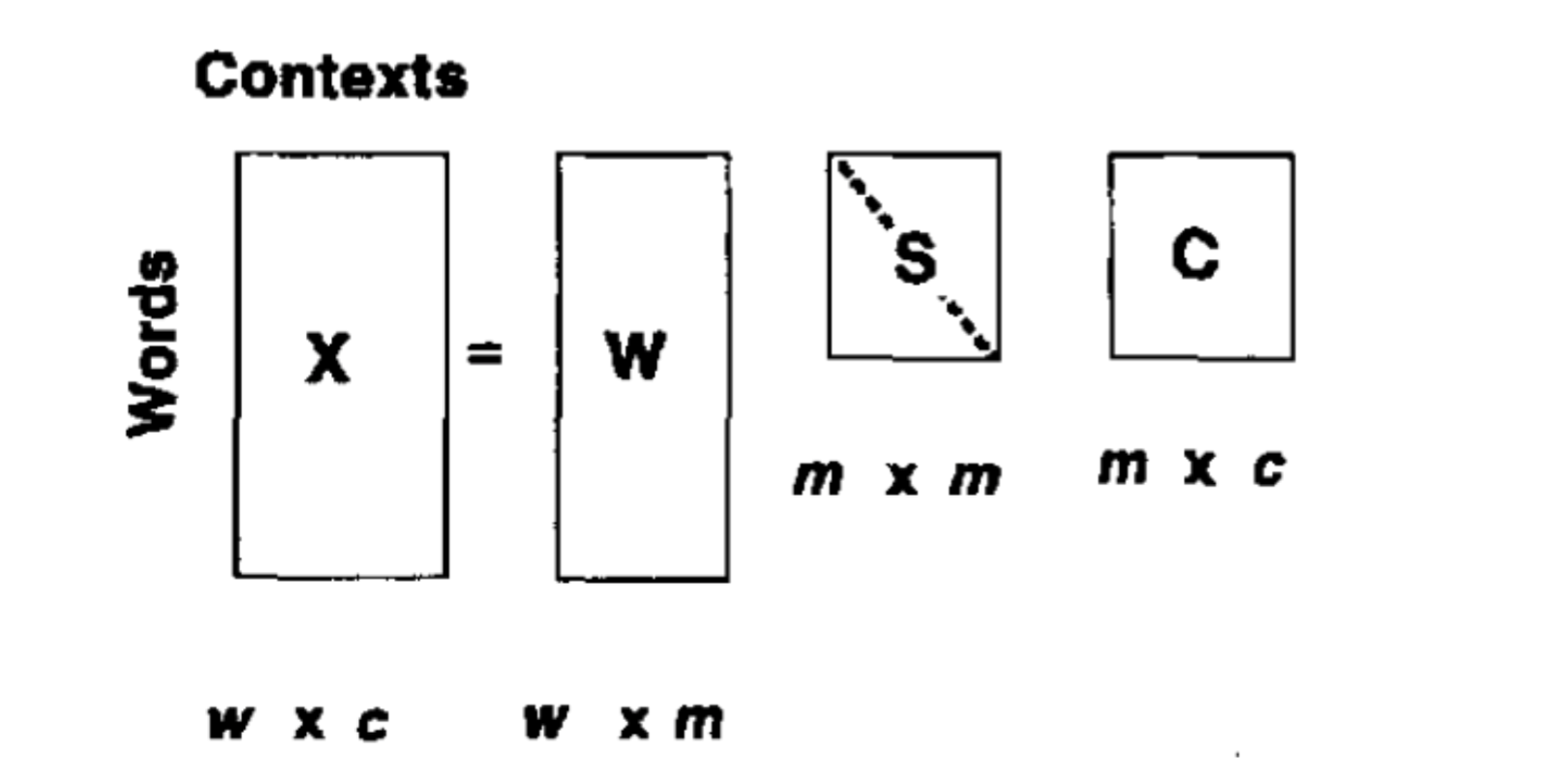
没必要保留所有的维度,我们可以只留 top k 个奇异值,比如说 300,结果是对原始 X 的最小二乘近似。我们也不需要做乘法,直接用 W 表示就好了,W 的每一行,是一个 K 维的向量,来表示单词 W。
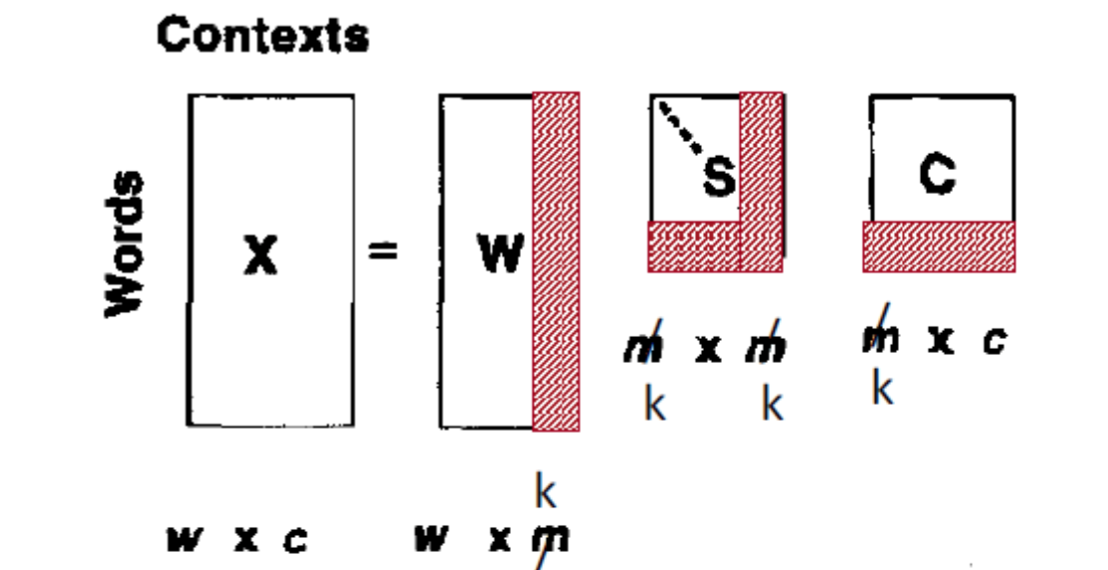
对于 LSA,我们一般会用 300 维,通常会给权重,local weight 就是取 log term frequency,global weight 就是取 idf 或者用 entropy 来衡量。
SVD 在词共现矩阵(term-term matrix)的应用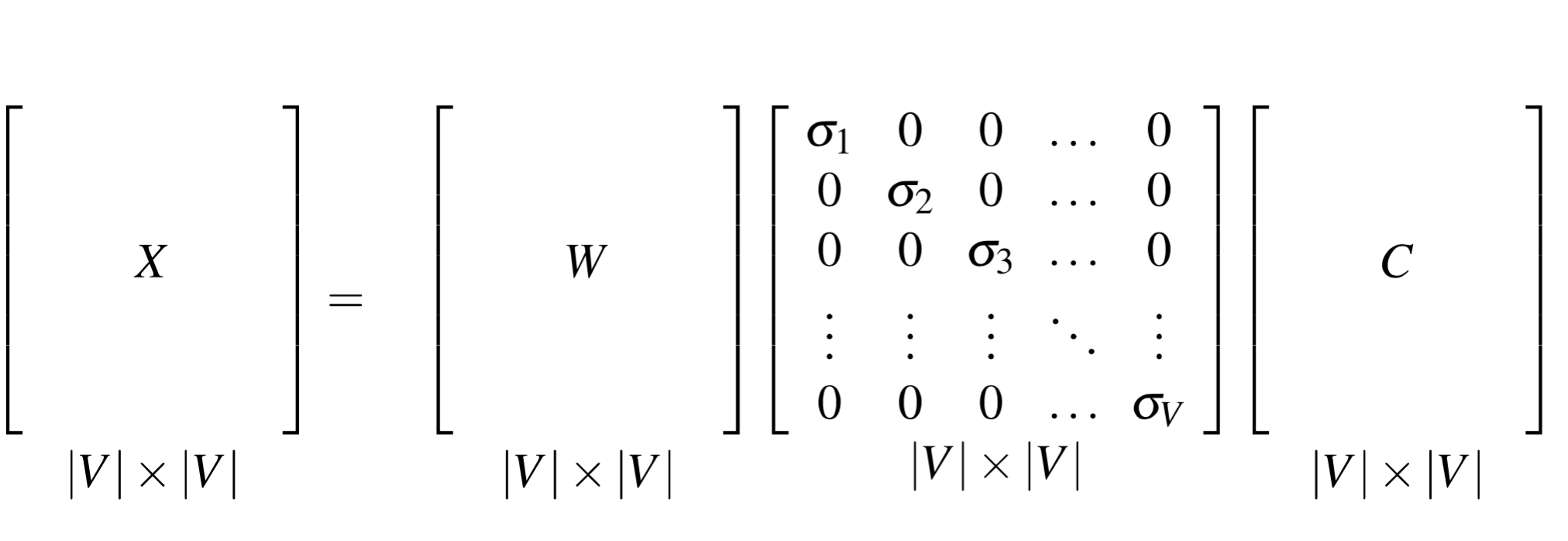
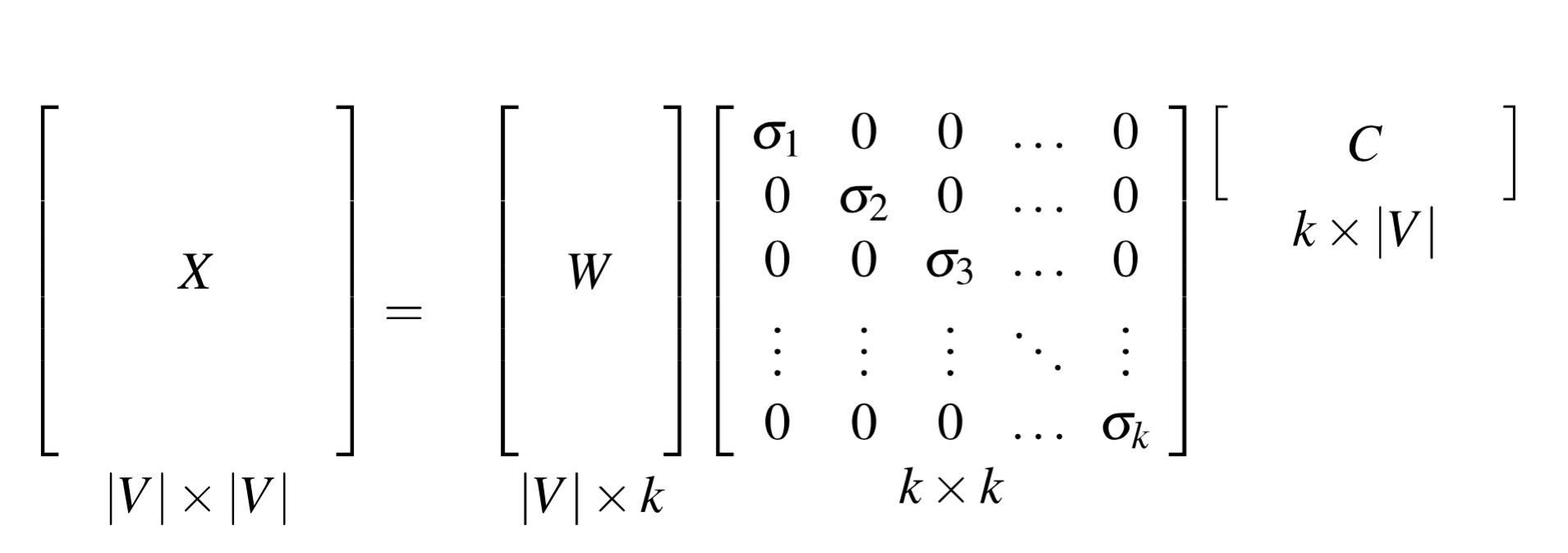
dense SVD embeddings 有时比 sparse PPMI 的效果好,尤其是在 word similarity 这类任务上。主要原因是
- dense SVD embeddings 进行了去噪,丢掉了低维的,可能不重要的信息
- 截断有助于提高泛化能力
- 相对较小的维度有利于分类器来训练权重
- 更好的捕获 higher order 共现信息
Neural Language Model
Word2Vec 的算法,Skip-grams 和 CBOW,见 词向量总结笔记(简洁版)
GloVe vs. Word2vec
学习词向量的两种方式,一种是用 Global matrix factorization methods,对词共现矩阵进行 factorization,如 LSA,另一种是用 local context window methods,如 Skip-gram 之类。然而,两种方法各有利弊,LSA 利用了统计数据,但是在单词相似性的任务上表现相对很差,是一个次优的向量空间结构,而 Skip-gram 等方法在单词相似性的任务上表现很好,但没有利用整个语料库的统计数据,因为它只对局部的上下文进行训练,而不是基于全局的共现矩阵。
GloVe 和 Word2vec 是现在常用的两种 word vector 方法/工具,两者最为显著的不同,是 word2vec 认为所有 co-occurrences 的权重都应该是相同的,而 GloVe 认为权重不应该相同,所以 GloVe 提出了 weighted least squares regression model,用加权最小二乘法来最小化两个词的向量点积与它们共现次数的对数之间的差异。事实上,GloVe 的作者表明两个词共现概率的比值(而不是它们的共现概率本身),更适合作为向量差来编码信息。
这两者在大部分 NLP 任务中的表现其实差不多,然而 GloVe 比 Word2Vec 多了个优势,它更容易来做并行化,也就是,更加容易训练更多的数据。
关于 count-based model 和 predictive model,具体的区别见 Don’t count, predict! A systematic comparison of context-counting vs. context-predicting semantic vectors。两个模型都会学习单词的共现特征,不同的是,predictive model 训练一个神经网络,预测周围的词语/目标词,优化损失函数(the loss of predicting the target words from the context words given the vector representations),而 count-based model 首先对整个语料库建立一个共现矩阵,然后对这个矩阵做 Factorization,以此产生低维向量,通常,是通过最小化 “reconstruction loss” 来实现的。
“reconstruction loss”: tries to find the lower-dimensional representations which can explain most of the variance in the high-dimensional data. In the specific case of GloVe, the counts matrix is preprocessed by normalizing the counts and log-smoothing them. This turns out to be A Good Thing in terms of the quality of the learned representations.
2014 年,Baroni 等人表明 predictive model 几乎在所有的任务中都优于 count-based model,然而,当 GloVe 被 Levy 等人认为是一个预测模型时,它显然是正在分解一个词语上下文共现矩阵,更接近于诸如主成分分析(PCA)和潜在语义分析(LSA)等传统的方法,不止如此,Levy 等人还表示 word2vec 隐晦地分解了词语上下文的 PMI 矩阵。
另外提几点,来自 Illinois 的 Jiaqi Mu 做的分享中提到的,关于两者的一些统计数据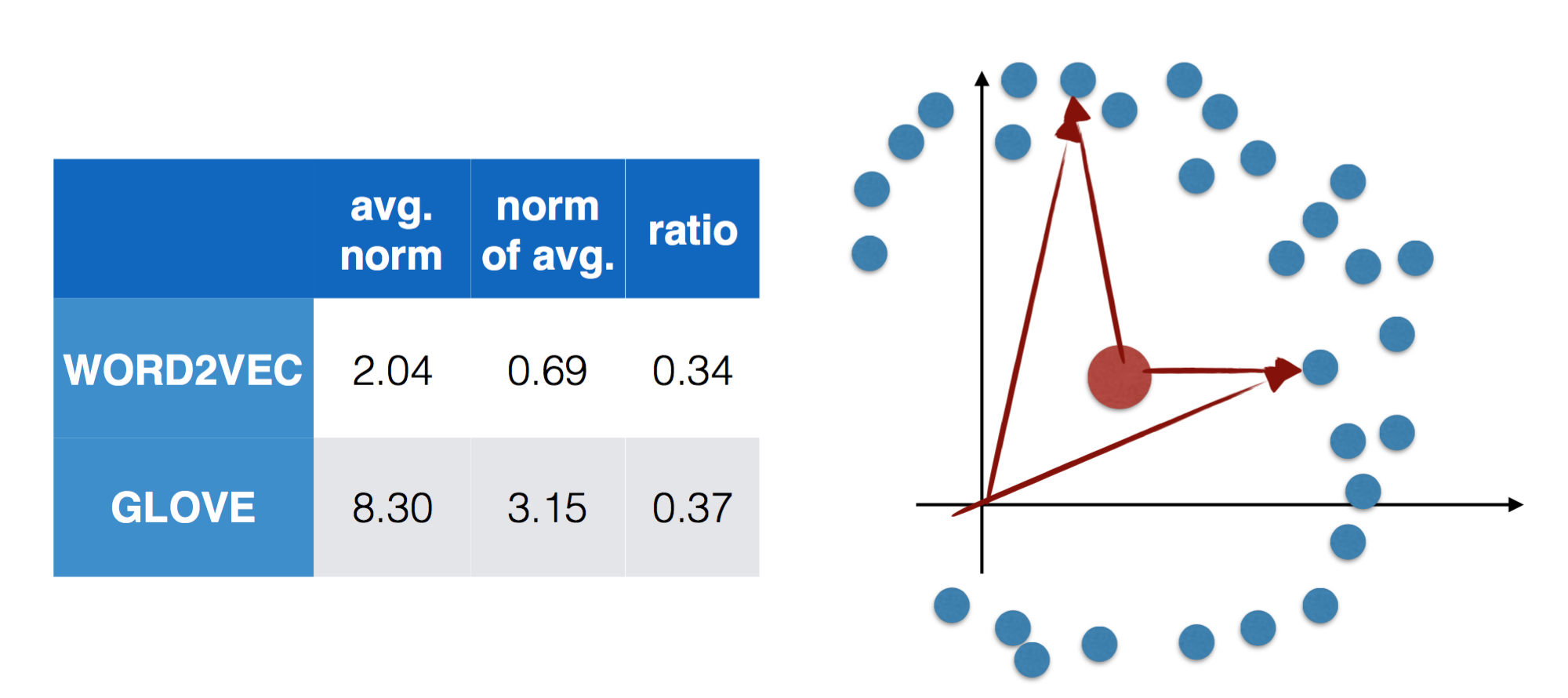
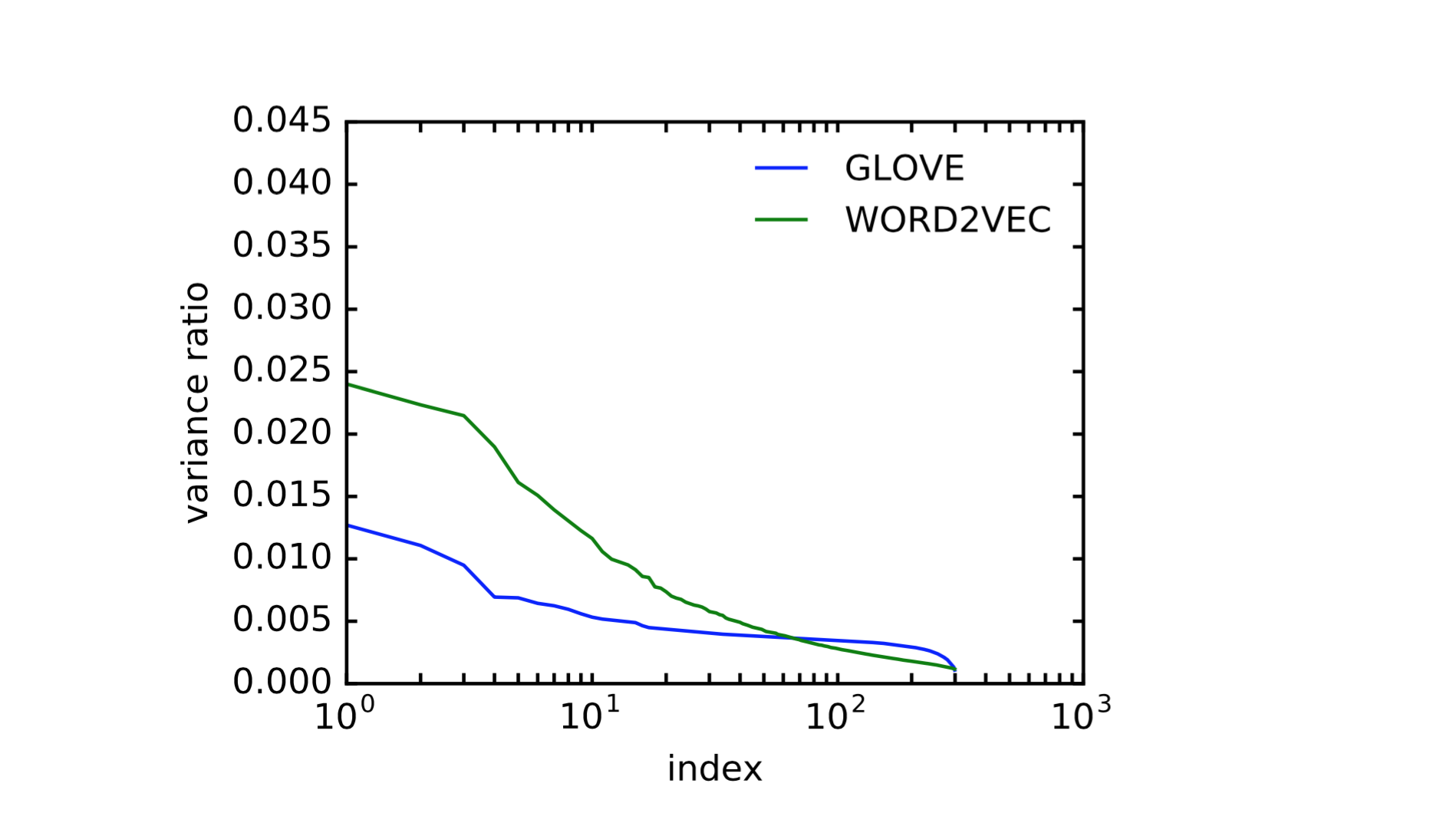
从这些学习到的词向量来看,它们并不是 0 均值的,词向量聚集在均值周围,均值模长是词向量模长的 1/3 左右,我们知道向量之间的相似度是由夹角来描述的,如果有偏移,对相似度会有影响。另一方面,它们不是各向同性的,也就是说,向量并不是均匀分布在整个空间内,对空间的利用并不充分,有可能在某个空间上聚集了更多的能量,Jiaqi Mu 针对这两点做了 postprocessing,移除了非 0 偏置,并用主成分分析算出哪些维度的能量比较集中,进行了降维,然后实验发现,neural network 本身就能学习去掉均值、去掉某些方向这类的操作(automatically learn the postprocessing operation)。
Brown clustering
在NLP 笔记 - Part of speech tags中提到过,就不多说啦。

