CMU 11611 的课程笔记。Language model 在别的课中不管是单机还是分布式都实现过好几次,然而却没有深入系统的研究过。
应用场景
Language model 通常有两类目标,一个是 计算句子或一系列单词出现的概率,另一个是 单词预测(word prediction),通常的应用场景有:
- Machine Translation
P(high winds tonite)>P(large winds tonite) - Spell Correction
The office is about fifteen minuets from my house
P(about fifteen minutes from)>P(about fifteen minuets from) - Speech Recognition
P(I saw a van) >> P(eyes awe of an) - +Summarization,question,answering,etc.
文本预处理问题
标点
是否把标点算为单词,取决于不同的任务。对于诸如 语法检查、拼写错误检查、作者辨认 这样的任务,标点符号的位置是很重要的。因此这些应用中经常把标点符号看做单词。
大小写
大多数统计应用来说,是忽略大小写的,尽管有时候也把大写作为个别的单独特征来处理(在拼写错误更正或词类标注中)
屈折形式
- 词形(wordform): 在语料库中以屈折形式出现的单词形式
- 词目(lemma): 具有同一词干、同一主要词类、同一词义的词汇形式的集合
- 型(type): 语料库中不同单词的数目
- 例(token): 使用中的单词数目
当前大多数基于 N-gram 的系统都是以词形(wordform)为基础的。所以,cat 和 cats 要分别处理为两个单词。然而在很多领域中,我们想把 cat 和 cats 看成同一个抽象单词的实例,可以用词典,词典中不包含有屈折变化的形式。用词典来计算词目比计算词形更方便。
口语语料库
- 话段(fragment): 相当于句子
- 片段(fragment): 一个单词在中间被拦腰切开而形成的,如 main-mainly
- 有声停顿(filled pause): 如 um, uh
取决于应用的具体情况,如果在自动语音识别的基础上建立一个自动听写系统,我们可能需要把片段剔除。而有声停顿,更倾向于被当成单词来处理,um 和 uh 的意思稍有不同,一般当说话人胸有成竹要说某个话段时,他就 um,而当说话人想说但还没找到恰当的单词来表达时,就用 uh,另外,uh 经常可以用来作为预测下一个单词的线索,所以很多系统都把它当做一个单词来处理。
简单的(非平滑的) N 元语法
数学基础
Chain Rule
$$P(x_1,x_2,x_3,…,x_n) = P(x_1)P(x_2|x_1)P(x_3|x_1,x_2)…P(x_n|x_1,…,x_n,1)$$
Markov Assumption
N-gram 的基本假设是 一个单词的概率只依赖于它前面单词的概率,这也就是 马尔可夫假设。举个例子:
P(the | its water is so transparent that) $\approx$ P(the | that)
P(the | its water is so transparent that) $\approx$ P(the | transparent that)
事实上,马尔可夫链就是一种加权有限状态自动机,加权 FSA 的下一个状态总是依赖于他前面有限的历史(有限自动机的状态数目总是有限的),bigram 可以看成是每个单词只有一个状态的马尔可夫链,也称为一阶马尔可夫模型,N-gram 称为 N-1 阶马尔可夫模型。
$$P(w_1w_2…w_n) \approx \sum_iP(w_i|w_{i-k}…w_{i-1})$$
再转换下
$$P(w_1|w_1w_2…w_n) \approx \sum_iP(w_i|w_{i-k}…w_{i-1})$$
Maximum Likelihood Estimate
很简单啦,以 Bigram 为例,就是 $P(w_i|w_{i-1})={count(w_{i-1},w_i) \over count(w_{i-1})}$
Models
注意,在下面的模型中,我们用到了 padding,所有 N-gram 模型都用了一个特殊符号来标记句子的结束(STOP_SYMBOL),N>1 时,另外用一个特殊符号来标记句子的开始(START_SYMBOL),来方便计算。
Uniform Model
假定语言中的任何一个单词后面可以跟随该语言中的任何一个单词,且概率是相等的。如果英语中有 100,000个单词,那么任何一个单词后面跟随其他任何单词的概率将是 1/100,000,即 0.00001
Unigram Model
任何一个单词后面可以跟随着其他任何单词,但后面一个单词按照它正常的频度来出现,所以可以根据相对频度对下面将要出现的单词指派一个概率分布的估值。
$$
\begin{aligned}
p(W=w) & = p(W_1=w_1, W_2=w_2,…,W_{L+1}=stop) \\
& = (\prod^L_{l=1}p(W_l=w_l))p(W_{L+1}=stop) \\
& = (\prod^L_{l=1}p(w_l))p(stop)
\end{aligned}
$$
Full History Model
如果不是简单地看单词相对频度,而是要看单词对于给定历史的条件概率,那么就有了 full history model。
Every word is assigned some probability, conditioned on every history.
$$
\begin{aligned}
p(W=w) & = p(W_1=w_1, W_2=w_2,…,W_{L+1}=stop) \\
& = (\prod^L_{l=1}p(W_l=w_l|W_{1:l-1}=w_{1:l-1}))p(W_{L+1}=stop|W_{1:L}=w_{1:L}) \\
& = (\prod^L_{l=1}p(w_l|history_l))p(stop|history_L)
\end{aligned}
$$
N-Gram Model
Every word is assigned some probability, conditioned on a fixed-length history(n-1)
$$
\begin{aligned}
p(W=w) & = p(W1=w1, W2=w2,…,W_{L+1}=stop) \\
& = (\prod^L_{l=1}p(W_l=w_l|W_{l-n+1:l-1}=w_{l-n+1:l-1}))p(W_{L+1}=stop|W_{L-n+1:L}=w_{L-n+1:L}) \\
& = (\prod^L_{l=1}p(w_l|history_l))p(stop|history_{L+1})
\end{aligned}
$$
以 Bigram 为例,假设 <s> 为 START_SYMBOL,</s> 为 STOP_SYMBOL
$$p(w^1_L)=\prod^L_{l=1}P(w_l|w_{l-1})p(stop|w_{L+1})$$
文本:
那么有
第一句话的概率就是
对数(Logprob)
由于概率都小于 1,相乘的概率越多,所有概率的乘积就越小,这样就会有数值下溢(underflow)的危险,所以习惯上会采用对数空间来进行计算(加法比乘法快),给每个概率取对数再相加,最后再取结果的反对数。
归一化(Normalizing)
归一化,就是用某个总数来除,使最后得到的概率的值处于 0 和 1 之间,以保持概率的合法性,也就是:
$$p(w_n|w_{n-1})={C(w_{n-1}w_n) \over \sum_wC(w_{n-1}w)}$$
要注意的一个优化是,给定单词 $w_{n-1}$ 开头的所有二元语法的计数必定等于该单词 $w_{n-1}$ 的一元语法的计数,也就是说,对一般的 N-gram,参数估计为:
$$p(w_n|w^{n-1}_{n-N+1})={C(w^{n-1}_{n-N+1}w_n) \over C(w^{n-1}_{n-N+1})}$$
Unknown word
对 unknown word 的处理,一般我们建一个固定大小的 lexicon(比如说语料库里 frequency>5 的单词),再新建一个 token <UNK>,不在 lexicon 里的 token (也就是 frequency<5 的单词)都编译成 <UNK>,然后把 <UNK> 当做普通单词处理。
N-gram 对语料库的敏感性
直观上的两个重要事实:
- N 越大 N-gram 的精度也应相应增加
训练模型的上下文越长,句子连贯性也就越好 - N-gram 性能强烈依赖于它们的语料库(特别是语料库的种类和单词的容量)
为了很好的在统计上逼近英语,需要一个规模很大、包含不同种类、覆盖不同领域的语料库
平滑(Smoothing)
每个特定的语料库都是有限的,从任何训练语料库得到的 bigram 矩阵都是稀疏的(sparse),存在着大量的零概率 bigram 的场合,当非零计数很小时,MLE 会产生很糟糕的估计值。平滑就是给某些零概率和低概率的 N-gram 重新赋值并给它们指派非零值。
加 1 平滑(add-one smoothing)
也叫 Laplace smoothing,假设 we saw each word one more time than we did
MLE estimate:
$$P_{MLE}(w_i|w_{i-1})={c(w_{i-1}w_i) \over c(w_{i-1})}$$
Add-1 estimate:
$$P_{Add-1}(w_i|w_{i-1})={c(w_{i-1}w_i)+1 \over c(w_{i-1})+V}$$
加 1 平滑是一种很糟糕的算法,与其他平滑方法相比显得非常差,然而我们可以把加 1 平滑用在其他任务中,如文本分类,或者非零计数没那么多的情况下。
Good-Turing smoothing
基本思想: 用观察计数较高的 N-gram 数量来重新估计概率量大小,并把它指派给那些具有零计数或较低计数的 N-gram
首先理解一个概念
Things seen once: 使用刚才已经看过一次的事物的数量来帮助估计从来没有见过的事物的数量。举个例子,假设你在钓鱼,然后抓到了 18 条鱼,种类如下:10 carp, 3 perch, 2 whitefish, 1 trout, 1 salmon, 1 eel,那么
下一条鱼是 trout 的概率是多少?
很简单,我们认为是 1/18
那么,下一条鱼是新品种的概率是多少?
不考虑其他,那么概率是 0,然而根据 Things seen once 来估计新事物,概率是 3/18
在此基础上,下一条鱼是 trout 的概率是多少?
肯定就小于 1/18,那么怎么估计呢?
在 Good Turing 下,
$$P^*_{GT} (things \ with \ zero \ frequency)={N_1 \over N_2}$$
$$c^* = {(c+1)N_{c+1} \over N_c}$$
Nc = the count of things we’ve seen c times
所以,c=1时,
$C^* (trout)=2*{N2 \over N1} = 2*1/3 = 2/3$
$P^* (trout)={2/3 \over 18}={1 \over 27}$
Backoff(回退)
直观的理解,如果没有 3gram,就用 bigram,如果没有 bigram,就用 unigram。
Linear Interpolation(线性差值)
我们看这样一种情况,如果 c(BURNISH THE) 和 c(BURNISH THOU) 都是 0,那么在前面的平滑方法 additive smoothing 和 Good-Turing 里,p(THE|BURNISH)=p(THOU|BURNISH),而这个概率我们直观上来看是错误的,因为 THE 要比 THOU 常见的多,$p(THE|BURNISH) \ ge p(THOU|BURNISH)$ 应该是大概率事件。要实现这个,我们就希望把 bigram 和 unigram 结合起来,interpolate 就是这样一种方法。
用线性差值把不同阶的 N-gram 结合起来,这里结合了 trigram,bigram 和 unigram。用 lambda 进行加权
$$
\begin{aligned}
p(w_n|w_{n-1}w_{n-2}) & = \lambda_1 p(w_n|w_{n-1}w_{n-2}) \\
& + \lambda_2 p(w_n|w_{n-1}) \\
& + \lambda_3 p(w_n)
\end{aligned}
$$
$$\sum_i \lambda_i=1$$
怎样设置 lambdas?
把语料库分为 training data, held-out data, test data 三部分,然后
- Fix the N-gram probabilities(on the training data)
- Search for lambdas that give the largest probabilities to held-out set:
$logP(w_1…w_n|M(\lambda_1…\lambda_k))=\sum_ilogP_M(\lambda_1…\lambda_k)(w_i|w_{i-1})$
这其实是一个递归的形式,我们可以把每个 lambda 看成上下文的函数,如果对于一个特定的 bigram 有特定的计数,假定 trigram 的计数是基于 bigram 的,那么这样的办法将更可靠,因此,可以使 trigram 的 lambda 值更高,给 trigram 更高权重。
$$
\begin{aligned}
p(w_n|w_{n-1}w_{n-2}) & = \lambda_1 (w^{n-1}_{n-2})p(w_n|w_{n-1}w_{n-2}) \\
& + \lambda_2 (w^{n-1}_{n-2})p(w_n|w_{n-1}) \\
& + \lambda_3 (w^{n-1}_{n-2})p(w_n)
\end{aligned}
$$
通常 $\lambda w^{n-1}_{n-2}$ 是用 EM 算法,在 held-out data 上训练得到(held-out interpolation) 或者在 cross-validation 下训练得到(deleted interpolation)。$\lambda w^{n-1}_{n-2}$ 的值依赖于上下文,高频的上下文通常会有高的 lambdas。
更多平滑见 Stanford Language Modeling
Evaluation
在训练集上训练参数,在测试集上测试 performance,那么之后怎么来评估模型呢?最好的办法当然是 外部评价方法 是把两个模型放到具体的任务环境中(spelling corrector/speech recognizer/MT system),然后测试模型,比较两个模型的准确率。然而这种方法比较麻烦,所以一般还是用 内部评价方法,perplexity 来评估模型,尽管它不是一个很好的估计(除非真实情况就是 test data 和 training data 是非常相似的),但好歹也是有用的,一般用于 pilot experiments 中。
Perplexity
Perplexity is the inverse probability of test set normalized by the number of words
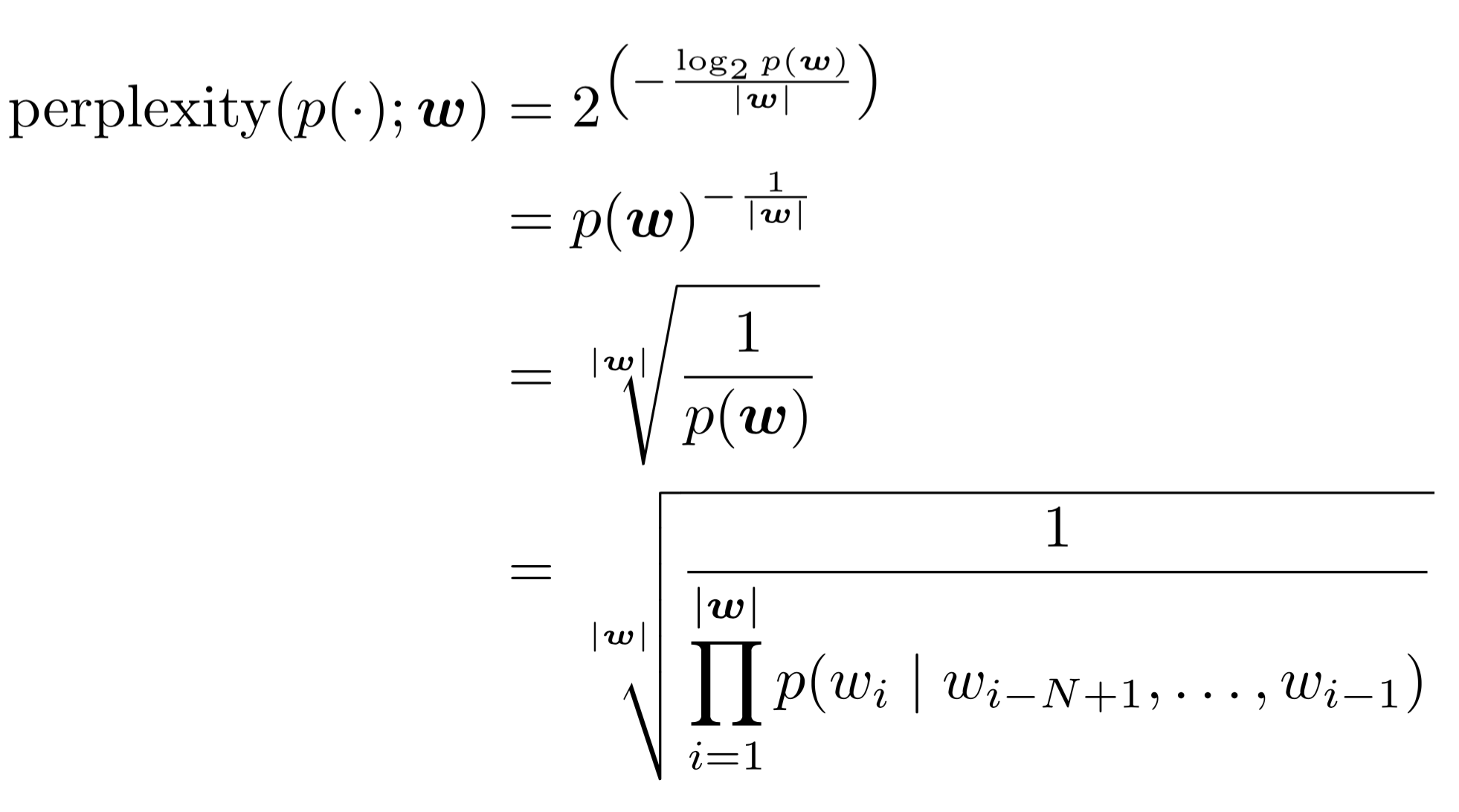
第二个式子用了 chain rule,第三个式子是 bigram 的情况。举个例子来理解 perplexity,如果一个句子由 0-9 位数字随机生成,那么这个句子的 perplexity 是多少?假定每个 digit 出现的概率都是 1/10。=> PP(W)=(1/10)^-1=10
我们的目标是最小化 perplexity,lower perplexity=better model。
理论基础是 熵(entropy),熵在 NLP 中是非常有价值的,可以用来度量一个特定语法中的信息量是多少,度量给定语法和给定语言的匹配程度有多高,预测一个给定的 N-gram 中的下一个单词是什么,如果给定两个语法和一个语料库,我们还可以使用熵来估计哪个语法和语料库匹配的更好…
小结
- Relative frequencies (count & normalize)
- Transform the counts:
Laplace/“add one”/“add λ”
Good-Turing discounting - Interpolate or “backoff”:
With Good-Turing discounting: Katz backoff – “Stupid” backoff
Absolute discounting: Kneser-Ney
更复杂的一些 N-gram 方法
- cache LM(Kuhn and de Mori 1990)
- 用 long-distance trigger 来替代局部 N-gram(Rosenfeld, 1996; Niesler and Woodland, 1999; Zhou and Lua, 1998)
- 可变长 N-gram(variable-length N-gram)(Ney et al., 1994; Kneser, 1996; Niesler and Woodland, 1996)
- 用语义信息来丰富 N-gram
基于潜在语义索引(latent semantic indexing)的语义词联想方法(Coccaro and Jurafsk, 1988; Bellegarda, 1999)
从联机词典和类属词典中提取语义信息的方法(Demetriou et al., 1997) - 基于类的 N-gram
- 基于更结构化的语言知识的语言模型(如概率剖析)
- 使用当前话题的知识来提升 N-gram(Chen et al., 1998; Seymore and Rosenfeld 1997; Seymore et al., 1998; Florian and Yarowsky 1999; Khudanpur and Wu, 1999)
- 使用言语行为和对话知识来提升 N-gram

