全连接神经网络
一个浅层的神经网络,如下图其实就可以看作一个 logistic regression 模型加上非线性激励函数。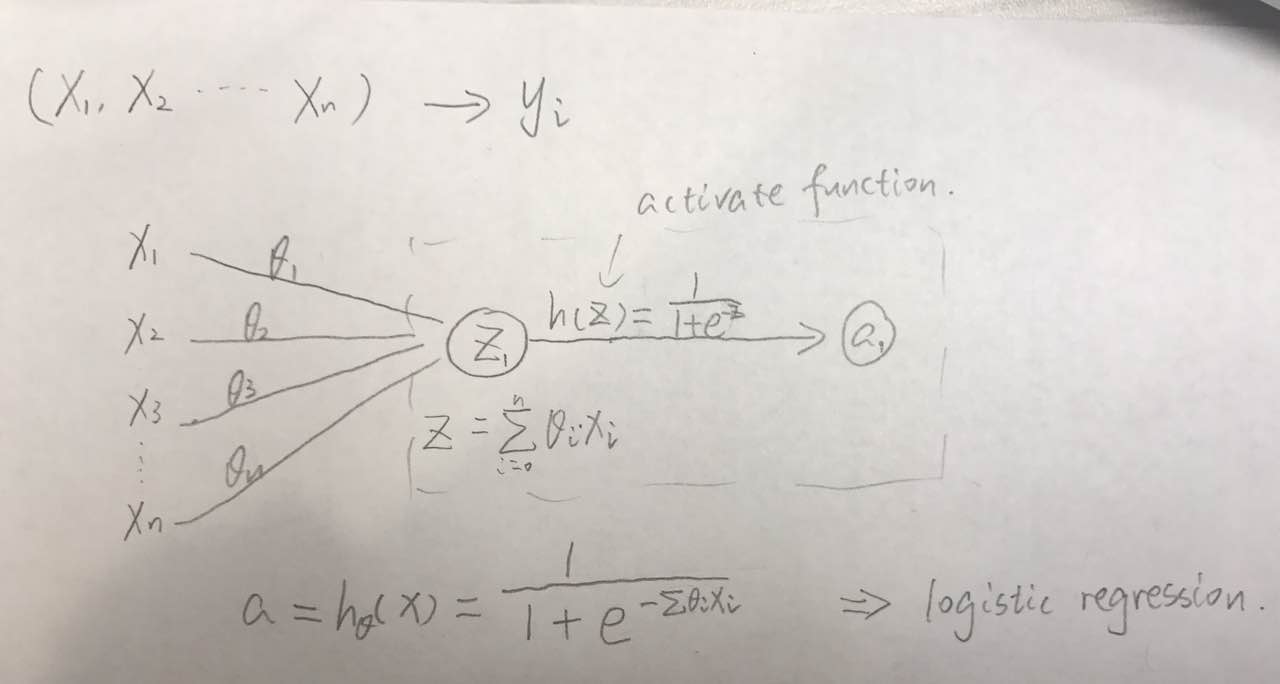
一个神经元的组成:
- 输入:n 维向量
- 线性加权:$z=\sum^n_{i=1}w_ix_i+b$
- 激活函数:a=h(z),要求非线性,容易求导
- 输出值:a(标量)
当然我们可以加 z2, z3, a2, a3… 输入是 x1,x2…xn,输出是 a1,a2…am,如果给一个神经元,就是或 0 或 1 的输出,如果给多个,就从 logistic 回归变成了 softmax 回归。
一个输入,若干个中间层(可能是全连接/非全连接网络),最后输出层,如果要做分类,就可以给一个或多个全连接网络(可以看作是 softmax)。
激活函数
如果不用激活函数,或者说激活函数是f(x) = x,那么在这种情况下你每一层输出都是上层输入的线性函数,很容易验证,无论你神经网络有多少层,输出都是输入的线性组合,与没有隐藏层效果相当,来个例子,假设
X1=W0*X0
X2=W1*X1
Y=W2*X2
那么,线性矩阵相乘,可以直接简化为一层:Y=W2*W1*W0*X0=W3*X0,为什么还要用网络?
所以,有线性回归网络吗?没有!
正因为上面的原因,我们才要引入非线性函数作为激励函数,这样深层神经网络就有意义了(不再是输入的线性组合,可以逼近任意函数)。最早的想法是 sigmoid 函数或者 tanh 函数,输出有界,很容易充当下一层输入。
性质
激活函数通常有如下一些性质:
非线性: 当激活函数是线性的时候,一个两层的神经网络就可以逼近基本上所有的函数了。但是,如果激活函数是恒等激活函数的时候(即f(x)=x),就不满足这个性质了,而且如果MLP使用的是恒等激活函数,那么其实整个网络跟单层神经网络是等价的。
可微性: 当优化方法是基于梯度的时候,这个性质是必须的。
单调性: 当激活函数是单调的时候,单层网络能够保证是凸函数。
f(x)≈x: 当激活函数满足这个性质的时候,如果参数的初始化是random的很小的值,那么神经网络的训练将会很高效;如果不满足这个性质,那么就需要很用心的去设置初始值。
输出值的范围: 当激活函数输出值是 有限 的时候,基于梯度的优化方法会更加 稳定,因为特征的表示受有限权值的影响更显著;当激活函数的输出是 无限 的时候,模型的训练会更加高效,不过在这种情况小,一般需要更小的learning rate.
这些性质,也正是我们使用激活函数的原因。
分类
Sigmoid
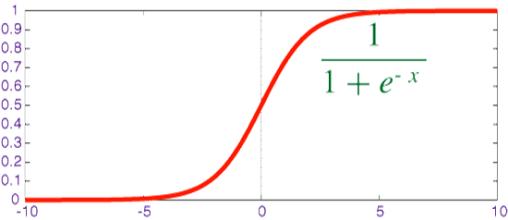
公式:
$$f(x)=sigmoid(x)={1 \over 1+e^{-x}}$$
对其求导
$$
\begin{aligned}
{df \over dx} & = -{1 \over (1+e^{-x})^2}(-e^{-x}) \\
& = {1 \over 1+e^{-x}} {e^{-x} \over 1+e^{-x}} \\
& = {1 \over 1+e^{-x}} {1+e^{-x}-1 \over 1+e^{-x}} \\
& = f(x)(1-f(x))
\end{aligned}
$$
Sigmoid 将数据映射到 [0,1]
缺点:
Sigmoids saturate and kill gradients.
- 梯度下降非常明显,且两头过于平坦,容易出现梯度消失的情况
当输入非常大或者非常小的时候(saturation),神经元的梯度是接近于0的,从图中可以看出梯度的趋势。所以,你需要尤其注意参数的初始值来避免 saturation 的情况。如果初始值很大的话,大部分神经元可能都会处在 saturation 的状态而把 gradient kill 掉,这会导致网络变的很难学习。 - 输出值域不对称(非0均值)
后一层的神经元将得到上一层输出的非 0 均值的信号作为输入,产生的一个结果就是:如果数据进入神经元的时候是正的(e.g. x>0 elementwise in f=wTx+b),那么 w 计算出的梯度也会始终都是正的。
tanh
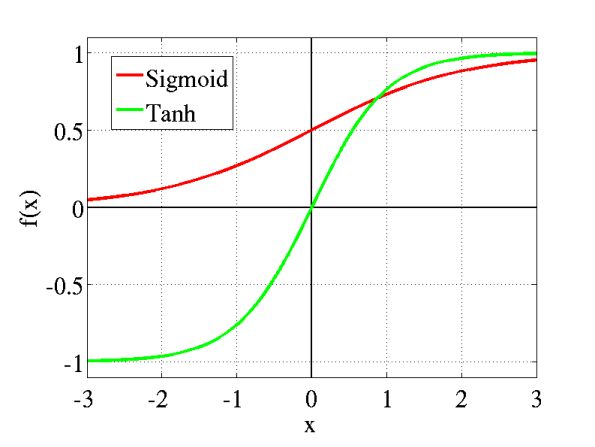
公式:
$$f(x)=tanh(x)={2 \over 1+e^{-2x}}-1$$
对其求导
我们知道 $tanh(x)={sinh(x) \over cosh(x)}$,所以对 f(x) 求导也就是对 ${sinh(x) \over cosh(x)}$ 求导。
$$
\begin{aligned}
{df \over dx} & = {cosh^2(x)-sinh^2(x) \over cosh^2(x)} \\
& = 1-tanh^2(x) \\
& = 1-f(x)^2
\end{aligned}
$$
tanh 将数据映射到 [-1,1],解决了 sigmoid 输出值域不对称问题,然而两头依旧过于平坦,梯度损失仍然明显。
ReLU(Rectified linear unit)
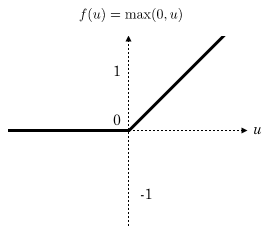
$$f(x)=max(0,x)$$
也就是 x<0 取0,否则取本身。
优点:
- 收敛速度比 sigmoid/tanh 更快
可能是因为它是linear,而且 non-saturating - 计算高效简单
相比于 sigmoid/tanh,ReLU 只需要一个阈值就可以得到激活值,ReLU具有所希望的特性,不需要输入归一化来防止它们达到饱和,也不用去算一大堆复杂的运算。 - 反向梯度没有损失
缺点:
- 正向截断负值,损失大量特征
- 训练时很“脆弱”,有 dead area
如,太高的 learning rate 配合上非常大的梯度流过一个 ReLU 神经元,更新过参数之后,这个神经元再也不会对任何数据有激活现象了。如果这个情况发生了,那么这个神经元的梯度就永远都会是 0.
实际操作中,如果 learning rate 很大,那么很有可能网络中的 40% 的神经元都”dead”了。
当然,如果你设置了一个合适的较小的 learning rate,这个问题发生的情况其实也不会太频繁。另外可以配合 Xavier 权重初始化方法,使用 adagrad 等方法自动调节 learning rate 来防止这种问题。
(-) Unfortunately, ReLU units can be fragile during training and can “die”. For example, a large gradient flowing through a ReLU neuron could cause the weights to update in such a way that the neuron will never activate on any datapoint again. If this happens, then the gradient flowing through the unit will forever be zero from that point on. That is, the ReLU units can irreversibly die during training since they can get knocked off the data manifold. For example, you may find that as much as 40% of your network can be “dead” (i.e. neurons that never activate across the entire training dataset) if the learning rate is set too high. With a proper setting of the learning rate this is less frequently an issue.
有实验说,大概 80%-90%的特征都会被截断,然而 ReLU 仍然是非常常用的激励函数,因为特征足够多。
Leaky ReLU
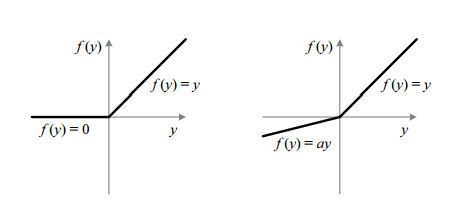
对 ReLU 的改进,解决 dying ReLU 的问题。x<0 时乘上一个 a 取较小的值,一般 a=0.01,可以保留更多的参数,反向梯度有部分损失。
为什么不变成 y=x?那不就回到了线性回归了嘛。
小结
一般现在都直接取 ReLU,然而如果使用 ReLU,一定要小心设置 learning rate,要注意不要让你的网络出现很多 “dead” 神经元,如果这个问题不好解决,那么可以试试 Leaky ReLU、PReLU、random ReLU 或者 Maxout。另外,现在主流的做法,会多做一步batch normalization,尽可能保证每一层网络的输入具有相同的分布,见Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift。
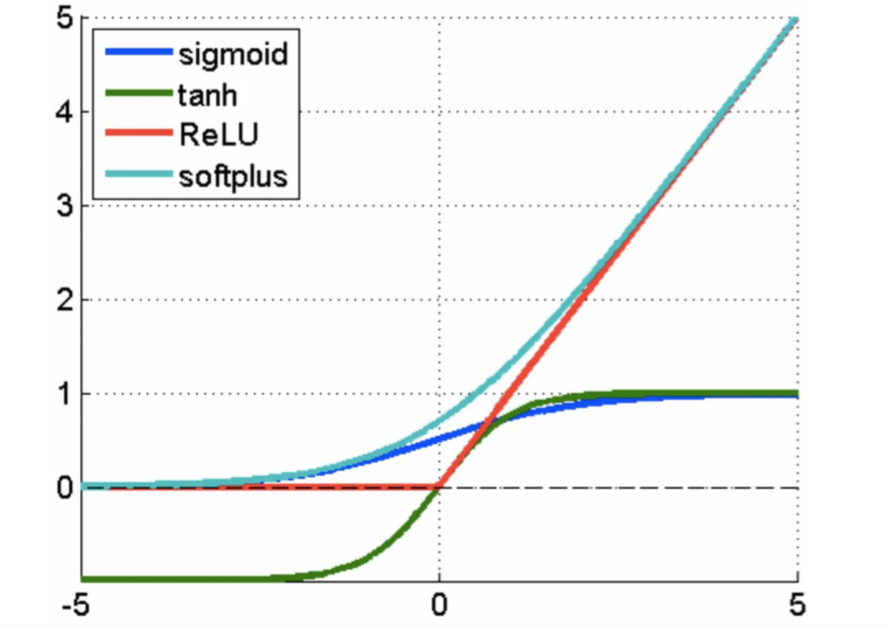
sigmoid 缺点:
- 两头过于平坦
- 输出值域不对称(非0均值)
tanh 缺点:
- 两头依旧过于平坦
ReLU:
- 收敛速度比 sigmoid/tanh 更快
- 计算高效简单
- Dead Area 中权重不更新(leaky ReLU 不存在 dead area)

