CMU 11642 的课程笔记。一个 query 可能表现了不同的信息需求，之前的相关性模型可能带来的结果是大多文档只能满足同一个信息需求，所以有些用户满意了，有些 user 抓狂了。我们希望检索到的 document 是能够 diverse 的，这样的话可以尽可能的满足不同用户的需求。这一章就讲了怎么实现 diversity。

Relevance based ranking model

之前的 相关性模型(Relevance based ranking model) 的目的是：

在每个 ranking 位置上最大化预期用户满意度
主要基于与原始查询的文本相似性

我们基于了这样一个假设：

each document is independent of other documents in the ranking

它带来的检索结果是：

主要关注最可能出现的 intent
适用于一些用户，但另一些用户可能不满意

如果这条 query 清楚的表达了 user intent，那么这种方法能得到最佳的结果。然而事实往往是，一条 query 可能会有多种解释或者多种 user intents，如果我们返回的 documents 表达的都是错误的 intent 怎么办？用户得不到任何相关文档！这是相当糟糕的体验。

E.g.,

multiple interpretations
Query: discovery channel store
– The Discovery Channel store homepage?
– Discovery Channel store locations?
– Toys and products sold by Discovery Channel stores?
– Products based on the Animal Planet program?
multiple tasks for the same interpretation
Query: Carnegie Mellon University
– Find the home page of CMU (Navigational)
– Find the location of CMU  (Location)
– Check recent news about CMU  (News)
– Find pictures of CMU (Pictures)

所以我们引入了 多样性 的概念。多样性是 健壮性(robustness) 和 相关性(relevance) 之间的权衡，它会

减少最有可能的 intent 的相关性
覆盖多个 intent 增加鲁棒性

下面描述了两个层次的多样性。

原始查询的解释(Interpretation of the original query)
- 这个查询是指什么？
- 用户想知道这个 query 的哪一个方面的信息？
每个解释的不同任务(Different tasks for each interpretation)
- 用户想要完成什么任务？图片？地图？视频？导航？

这一章我们集中讲 diversification of interpretations。

Diversification Algorithms

主要有两类算法。
Implicit

query intent 隐含在文档排名中
假设相似的文档涵盖了相似的 intent

Explicit

显性定义了 query intent
对文档重新排序，以便覆盖所有的 query intent

Implicit Methods

一些特征：

不需要关于可能存在的 query intent 的先验知识 - 因此称为“隐式”
选择与查询匹配的文档然后重新排序，产生多样性排名
不偏好任何 query intent
- 受欢迎的 intent 没有得到比 rare intent 更重要

Maximum Marginal Relevance (MMR)

主要思路：

• Use the query to retrieve a ranking R of documents
• Use MMR to rerank the top N documents (build a new ranking S)
  – Select the 1st document based on how well it satisfies the query
  – Select subsequent documents based on two criteria
    » How well it satisfies the query
    » How different it is from documents ranked above it

MMR 是贪心算法(greedy algorithm)。在每一个 step，都选择一个文档插入最后的 ranking list。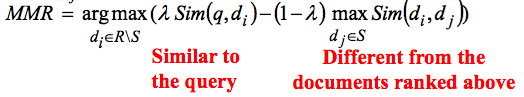

R: The initial ranking
S: Documents already selected for the diverse ranking
– Documents ranked above this position
Sim(di, dj): Similarity metric
– E.g., vector space model or Jensen-Shannon Divergence

举个例子，假设$\lambda = 0.6$，初始排名及其相关性分数如下

Initial Ranking
d1, 0.80
d2, 0.78
d3, 0.76
d4, 0.74
d5, 0.72
d6, 0.70

第一步，选择与 query 最相关的文档 d1，并从 R 中移除 d1

1 2	Diversified Ranking d1

计算剩余文档与 {d1} 的相似度和对应的多样性分数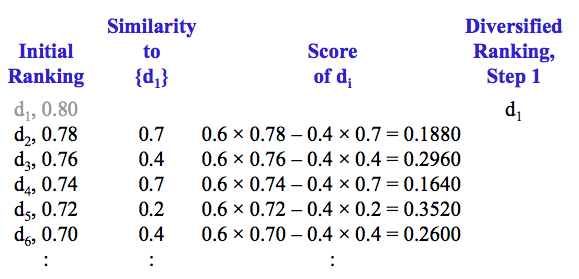

选择分数最高的文档作为多样性排名的第 2 篇文档，并从 R 中移除该文档

1
2
3

Diversified Ranking
d1
d5

分别计算剩余文档与已排序文档 {d1, d5} 的相似度，选相似度最大的值，计算 MMR 分数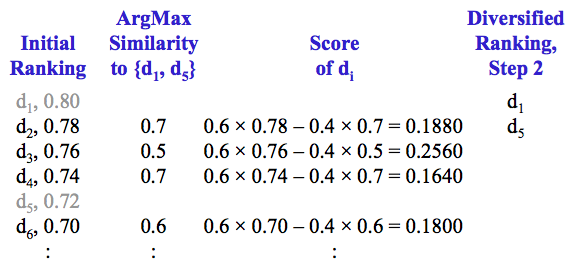

选择分数最高的文档作为多样性排名的第 3 篇文档，并从 R 中移除该文档

Diversified Ranking
d1
d5
d3

分别计算剩余文档与已排序文档 {d1, d5, d3} 的相似度，选相似度最大的值，计算 MMR 分数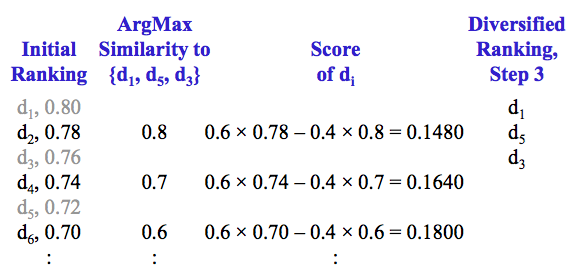

选择分数最高的文档作为多样性排名的第 4 篇文档，并从 R 中移除该文档

Diversified Ranking
d1
d5
d3
d6

分别计算剩余文档与已排序文档 d1, d5, d3, d6 的相似度，选相似度最大的值，计算 MMR 分数

选择分数最高的文档作为多样性排名的第 5 篇文档，并从 R 中移除该文档

Diversified Ranking
d1
d5
d3
d6
d2

Repeat until all documents in the initial ranking are added to the diversified ranking

所以就有了最后的排名 {d1, d5, d3, d6, d2}

MMR 也会用于其它的任务如文本摘要，因为它是符合摘要的基本要求的，即相关性和多样性的权衡。摘要结果与原文的相关性越高，摘要就接近全文中心意思，而多样性则使摘要内容更加的全面。直观和简单是这种方法最大的优点。

Similarity

关于相似度的衡量。
Anything-to-Anything Similarity
Vector space 可以比较任意两个向量的相似度，应用广泛，如聚类。
BM25 不能用 anything-to-anything similarity，但可以用 language modeling framework

Probabilistic Similarity
也有很多专门来计算 probability distribution similarity 的方法。KL divergence 就是其中很受欢迎的一种，然而它是不对称的，Jensen-Shannon Divergence 则是 KL divergence 的一个 symmetric and smoothed 的版本。

$$JS(x||y)={1 \over 2} KL(x||M) + {1 \over 2}KL(y|M)$$
$$M={x+y \over 2}$$

放到两个 document 的比较里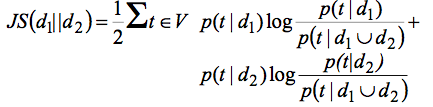

它也经常会用在 anything-to-anything similarity tasks 中。

Learning to Rank for diversification

MMR 是无监督的，而 Learning-to-Rank 就是 MMR 的 supervised 版本。

如果直接用传统的 learning-to-rank 模型来优化一个多样性指标 (e.g., α-NDCG)，也就是用和相同模型、相同特征，但是用基于多样性的训练数据（e.g., pointwise, pairwise, or listwise training data），来学习怎样产生 diversity ranking，会发生什么？

各种指标会得到不一致的结果
训练数据和测试数据会有不一样的 performance

Why?
因为传统 Le2R 忽略了文档之间的相关性，它只考虑 document-query 的相关性特征及 query independent 特征（e.g., pagerank），而缺少多样性特征如：

文档-文档的相似性特征
关于 sub-intents 的特征

因此，机器学习算法难以找到适用于多样性模型的合适的权重，相反，多样性的训练数据还会让学习模型感到困惑。所以有了一个解决方案： Relational-LeToR（R-LeToR），既考虑单个文档，又考虑文档与文档之间的关系，也就是说除传统 LeToR 需要的 relevance feature 之外，R-LeToR 还考虑了 relationship features，relationship 也就是相似度，计算的是候选文档与 higher-ranked documents 的相似度(和 MMR 的计算过程相似)

与传统 listwise Le2R 的区别是 ranking function 中多了 relational feature R：

Relational features

Relational features 由相关性函数得到，其输入是文档相似度。

文档间的相似度可以通过下面的方法计算：
文本相似度（Text similarity）:
– E.g. KL-Divergence of document language models
主题相似度（Topic similarity）:
– E.g. Cosine between docs’ topic distributions in topic models
类别相似度（Category similarity）:
– E.g. Overlap of docs’ categories in a predefined ontology
链接相似度（Link similarity）:
– E.g. whether docs have hyperlinks to each other
URL similarity:
– E.g. whether docs are from same website or not.

相关性函数可以是当前文档与 all higher-ranked doc 的：

最小相似度
平均相似度
最大相似度

Relational-ListMLE

ListMLE 是一种 ListWise LeToR，将一个 query 返回的整个文档排序列表作为输入，直接对排序结果列表进行优化，训练得到一个最优的评分函数，损失函数是 likelihood loss。关于 LeToR 的更多类型，这一篇不多做介绍。

ListMLE 可以轻松地处理各种 relational features。回忆下 ListMLE 的 sequential assumption

自上而下逐个挑选文档，这与 MMR 的 sequential assumption 相同
每个位置独立于先前的位置
与 ListMLE 不同的是，Relational-ListMLE 通过 relational features 打破了这种独立性假设

Relational-ListMLE 的生成过程是：

从候选文档中迭代产生新的排序
给定候选文档集合 Si = {d1, …, dn}
– 从 Si 中选择最适合出现在位置 i 上的文档 di
多提一句，p-ListMLE 也打破了这个假设

Relational-ListMLE 的生成过程是：

从候选文档中迭代产生新的 ranking
给定候选文档集合 Si = {d1, …, dn}
– 从 Si 中选择最适合出现在位置 i 上的文档 di

Learning and Ranking

学习的过程和 ListMLE 完全相同，损失函数仍然是 likelihood loss，用 SGD 优化。

排序时，因为文档依赖于之前的位置，无法像 ListMLE 一样直接计算 ranking score，所以

在 n 个位置的每一个位置上
» 从剩余的文档中选择 P(di|Si,w) 最高的文档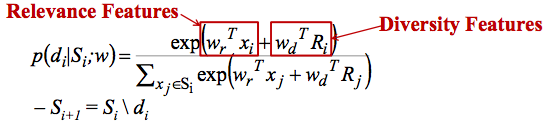 » 更新与其他文档的相似性特征 (O(n))

整个复杂度是 $O(n^2)$，而由于多样性算法是一种重排序方法，所以 n 不是很大，大多数情况下 n <1000

Performance

R-LeToR 是在 LeToR 基础上的一种最先进的技术，Relational-ListMLE 是唯一的一种监督的学习算法，因此可能比所有隐式和显式方法更好。然而正因为它是最近发表的，没有大量的证据，因此要小心使用。

Explicit Methods

Query intents (subtopics) discovery

怎么发现 query intents?

通过分析搜索日志。下一章会展开。
非常挑战，因为 query intent 都很 personal，不同的人有不同的解释，也有很多种 possible subtopics。
通常用对 top retrieved documents 进行聚类或 topic modeling 等方法来进行，但是效果并不好。
用已有的经验
– 由 TREC 提供的 query intents
– 由商业搜索引擎的 query suggestions／related queries 推断出的 query intents

Topic 1, type=faceted
• Query: obama family tree
• Description: Find information on President Barack Obama's family history, including genealogy, national origins, places and dates of birth, etc.
• Subtopic, type=nav: Find the TIME magazine photo essay "Barack Obama's Family Tree".
• Subtopic, type=inf: Where did Barack Obama's parents and grandparents come from?
• Subtopic, type=inf: Find biographical information on Barack Obama's mother.

注意两种类型的主题
Ambiguous: query 的不相关解释
– E.g., “michael jordan”, “avp”, “espn sports”

Faceted: query 的相关解释
– E.g., “arizona game and fish”, “obama family tree”

xQuAD

xQuAD(eXplicit Query Aspect Diversification (xQuAD))
Inputs
– An initial ranking
– 一组 query intents (e.g., from search engine suggestions)

Observation: 单个文档可能覆盖多个 intents，尤其是对 faceted queries 而言。

Key idea: 选择能够满足尽可能多的 uncovered intents 的文档
– Provide maximum coverage and minimum redundancy
– MMR did this implicitly
– xQuAD does it explicitly

xQuAD characteristics

需要一组显性的 query intents
允许单个文档满足多个 query intents
– 这些文档更有可能有高排名
多样性排名 equally 覆盖了每一个 intent
– 也可以对 intent 加权，但实验表明 uniform weights 是最好的
每个 query q 都需要运行 q + {q1, …, qk} 这么多查询语句
– 计算量略大
目前可用的最有效的方法之一

算法

Assumptions:
• 每个查询 q 都有 {q1, …, qk} 这么多 query intents
• 这些 query intents 都是相互独立的

R: Initial ranking (produced by some other method)
S: Diversified ranking (initially empty)
τ: Desired length of diversified ranking
$\lambda$: Balance between relevance and diversity

用相关性模型得到文档集合 R
计算文档分数，得到分数最高的文档 d*
从 R 中移除 d*
把 d* 加入 S

Selection criteria:
relevance 和 diversity 的平衡
$$(1-\lambda)P(d|q) + \lambda P(d,\overline S|q)$$

Diversity component:

实例

E.g.,
Step 1: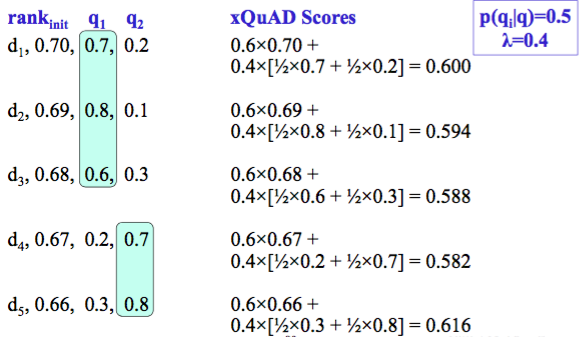

Step 2: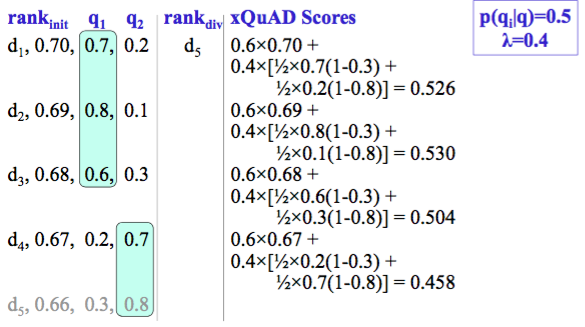

Step 3: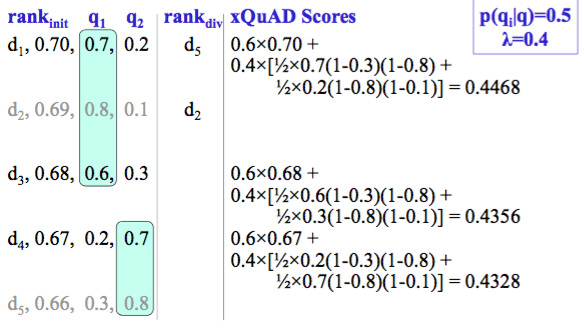

Step 4:

Step 5:

rank
xQuAD 偏好能够满足多个 intents 的文档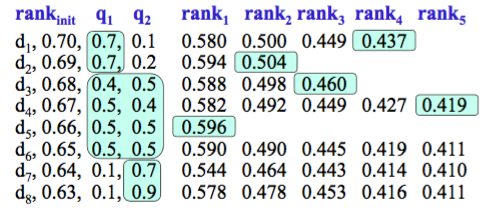

Weighting queries

Santos, et al 研究了 weighting queries 的三种方法

Uniform weights: 1 / |Q|
类似于 CRCS 资源排序算法的方法
– 与 ReDDE 相似
– 与 qi 匹配的 top-ranked documents 的数量相关
基于在商业搜索引擎中匹配的文档的相对数量

在 TREC 2009 的数据中，Uniform 被认为是最有效的。

Some research results

Related queries 并没有什么用
Suggested queries 更加有效

PM-2

Proportionality Model 2 (PM-2)
Inputs
– An initial ranking
– 一组 query intents (e.g., from search engine suggestions)

Observation: 用于发现 query intents 的算法，将发现许多稀少或不流行的 intents，高召回率。
– They shouldn’t get equal coverage in a diversified ranking

Key idea: 每个 subtopic 的文档数量应与每个 subtopic 的 popularity 成正比

最小化冗余
subtopic 的 coverage 可以更好地匹配用户需求

PM-2 characteristics

需要一组显性的 query intents
允许单个文档满足多个 query intents
– 这些文档更有可能有高排名
多样性排名按比例的覆盖每一个 intent
– 加权是可能的，但均匀的权重是最好的
每个 query q 都需要运行 q + {q1, …, qk} 这么多查询语句
可能计算量有点大
与 xQuAD 的相对性能取决于 datasets and explicit topics.

算法

PM-2 的思想其实来源自选举制的比例代表制的一种方法：Sainte-Laguë method

• At each rank r
  – 选择下一个必须覆盖的查询意图 qi，来保持排名中的意图比例覆盖率
  – 选择一个覆盖了意图 qi 的文档 d 
  » 同时，文档 d 也可能涵盖其他查询意图
  – 从原始排名 R 中删除文档 d
  – 把 d 加入多样化排名S

怎么计算下一个必须覆盖的查询意图 qi？
$$qt[i]={v_i\over 2s_i+1}$$

vi 是分配给这个意图的总文档数，实际等于 p(qi|q) x len(S)
si 代表已经分配给这个意图的文档，初始值为 0
最高的 quotient score 就对应下一个必须覆盖的意图

实例

E.g., 原始的相关性排名

假设：
λ=0.6
p(qi|q)=0.5
Ranking depth=8

Step 0: 初始化变量
计算分配给各个意图的文档数 votes v[i]
v[1] = 0.5×8 = 4
v[2] = 0.5×8 = 4

初始化 slots assigned s[i]
s[1] = 0
s[2]=0

Step 1，计算 quotient score
qt[1] = 4 / (2×0+1) = 4
qt[2] = 4 / (2×0+1) = 4

选择分数高的意图作为下一个必须覆盖的意图
$i^* = 1$

计算 PM2 分数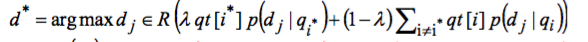

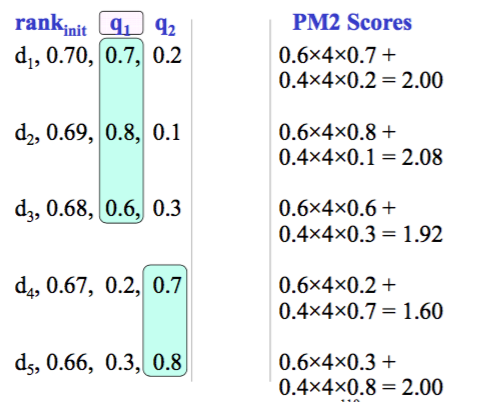
d2 wins!

Step 2
slots assigned s[i]
$$s[i]=s[i]+{P(d^*|q_i) \over \sum_qP(d^* |q_j)}$$
s[1] = 0+0.8/(0.8+0.1) = 0.89
s[2] = 0+0.1/(0.8+0.1) = 0.11

Quotient scores qt[i]
$$qt[i]={v_i\over 2s_i+1}$$
qt[1] = 4 / (2×0.89+1) = 1.44
qt[2] = 4 / (2×0.11+1) = 3.27

selected intent
$$argmax_i qt[i]$$
$i^* = 2$

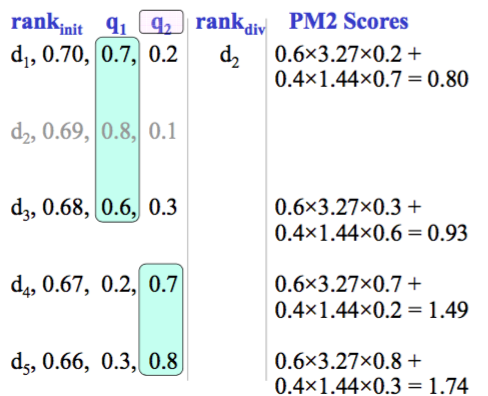
d5 wins!

Step 3
s[1] = 0.89+0.3/(0.3+0.8) = 1.16
s[2] = 0.11+0.8/(0.3+0.8) = 0.84

qt[1] = 4 / (2×1.16+1) = 1.20
qt[2] = 4 / (2×0.84+1) = 1.49

$i^*=2$

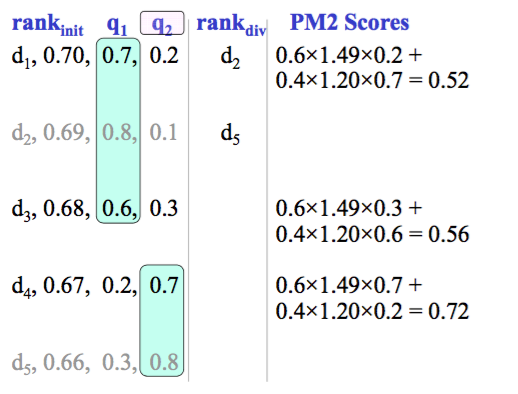
d4 wins!

Step 4
s[1] = 1.16+0.2/(0.2+0.7) = 1.38
s[2] = 0.84+0.7/(0.2+0.7) = 1.62

qt[1] = 4 / (2×1.38+1) = 1.06
qt[2] = 4 / (2×1.62+1) = 0.95

$i^* = 1$

d1 wins!

Repeat until all documents in the initial ranking are added to the diversified ranking

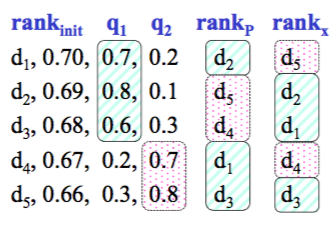
xQuAD vs pm2

xQuAD 选择涵盖多个 intents 的文档

给需要覆盖的 intents 赋予较高的权重

PM2 首先选择最需要覆盖的 intent

然后选择一个覆盖这个 intent 的文档
如果这个文档能覆盖其它 intents，那么给它加分

Summary

显式方法比 MMR 更有效。但需要一个 query intents 的外部来源，从网络搜索引擎获取的 intents 往往不能令人满意，因为它总是依赖于某一个组织。
xQuAD 和 PM-2 都是无监督的，效果不如有监督的模型 R-LeToR。

理想情况下，我们希望能结合这些方法的优点

无需使用外部资源
充分利用 subtopics
充分利用监督学习

Methods of identifying query intents

Commercial search engine suggestions
– Query suggestions > related queries
Still an open problem
– Very hard without search log

Characteristics

MMR: Implicit, unsupervised, penalizes redundancy
R-LeToR: Implicit, supervised, features to model redundancy
xQuAD: Explicit, unsupervised, penalizes redundancy
PM-2: Explicit, unsupervised, enforces proportionality

Performance:
R-LeToR > PM-2 ≈ xQuAD > MMR

Diversity Evaluation Metrics

Precision-IA@k

实际是 P@k 的变种。易于计算，易于理解。之前的模型里我们把 $q_i$ 当作 query 的第 i 个 term，而这里，$q_i$ 指代的是 query 的第 i 个 query intent。
假设 query q 有 n 个 query intents {q1, …, qn}，每个 intent 出现的概率是 p(qi | q)，一般来说，p(qi | q) 是均匀分布的，也就是 1/n 的概率，不需要 uniform。
计算步骤：

采用某种方法对 query q 检索到的文档进行排序
对每个 intent qi 计算 $P@k_{qi}$
对 P@kqi 求平均得到 Precision-IA@k
$Precision-IA@k=\sum_{qi}P(qi|q)P@k_{qi}$

评价：
通常一个好的策略是给满足了多个 intetns 的文档更高的优先级

能提高 Precision-IA @ k
用一个文档满足多个 intent 是降低风险的有效方法

α-NDCG

先来回顾下 NDCG 公式
$$NDCG@k = Z_k \sum_{i=1}^k{2^{R_i}-1 \over log(1+i)}$$

考虑了两点：

Gain from a document worth R(k) at rank k(based on relevance): $G@k=2^{R(k)}$
Discount for selecting a document at rank k(based on rank): $D@G={1 \over log_2(1+k)}$

特点：

考虑了每个文档的位置
允许了多值(multi-valued)的相关性评估
忽略了排名的多样性

它的变种 α-NDCG
Uses an intent-aware gain calculation

The gain vector for α-NDCG discounts intent redundancy

1-α controls the discount
If α=0.5
Value (j+1th reldoc, qi) = 0.5 ×Value (jth reldoc, qi)
(each document is worth 1⁄2 the previous document)