CMU 10601 的课程笔记。朴素贝叶斯思想即对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。

Generative and discriminative algorithms

Generative
try to model data, how data comes out, which disease cause with symptom with what probability - provide a profile for each disease
给定输入 x，生成模型可以给出输入和输出的联合分布 P(x,y)，生成模型的目标是求联合分布 P(x,y)，然后求出条件概率分布 P(Y|X) 作为预测的模型
- 以朴素贝叶斯为例，生成模型的求解思路是：联合分布——->求解类别先验概率和类别条件概率
- 联合分布能提供更多的信息，需要更多的样本和更多计算
- 收敛速度比较快，当样本数量较多时，生成模型能更快地收敛于真实模型。
- 生成模型能够应付存在隐变量的情况，比如混合高斯模型就是含有隐变量的生成方法。
- e.g. Naive Bayes, HMM
Discriminative
try to find mapping symptom -> disease reverse order
- 判别模型的求解思路是：条件分布——>模型参数后验概率最大——->（似然函数参数先验）最大——->最大似然
- 直接学习 P(Y|X)，节省计算资源，另外，需要的样本数量也少于生成模型
- 准确率往往较生成模型高
- e.g. Logistic Regression
- 实践中多数情况下判别模型效果更好

MLE and MAP

MLE(maximum likelihood estimate): choose $\theta$ that maximize D probability of observed data.
$$\theta = argmax \ P(D|\theta)$$

MAP(maximum a posterior estimate): choose $\theta$ that is most probable given prior probability and the data.
$$\theta = argmax \ P(\theta|D)=argmax \ {P(D|\theta)P(\theta) \over P(D)}$$

Bayesian statistics

主旨

Combine prior knowledge (prior probabilities) with observed data
Provides “gold standard” for evaluating other learning algorithms
Additional insight into Occam’s razor

图示

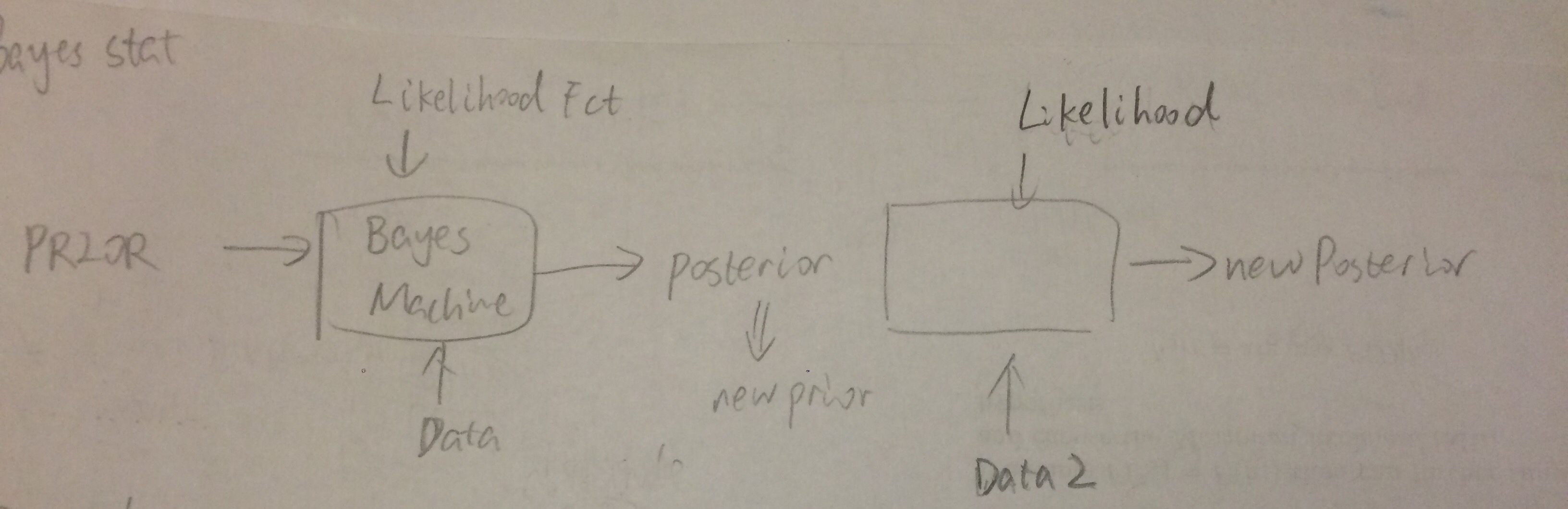
要记住的是: today’s posterior is tomorrow’s prior

公式

$$P(h|D)= {P(D|h)P(h) \over P(D)}$$
P(h) = prior probability of hypothesis h
P(D) = prior probability of training data D
P(h|D) = probability of h given D
P(D|h) = probability of D given h

推导非常简单

1 2	P(h,D) = P(h)P(D\|h) = P(D)P(h\|D)

一般来说，prior 不能是 0，否则 posterior 也会是 0 了。

Base rate neglect

Ignore prior in reasoning

If presented with related base rate information (i.e. generic, general information) and specific information (information only pertaining to a certain case), the mind tends to ignore the former and focus on the latter.

MAP (Maximum a posteriori)

判断 how well a hypothesis matches a data
$h \in H$
$$h_{MAP} = argmax P(h|D) = argmax {P(D|h)P(h) \over P(D)} = argmax P(D|h)P(h)$$

Example 1. Cancer

通过例子来说明
问题是：这个患者是否有癌症
条件是：

一个患者接受了一个检验，显示是阳性的(positive)。
这个检验返回的 correct positive 概率是 98%，correct negative 的概率是 97%。
人群中 0.008 的人可能会患这个癌症。

首先用熟悉符号表示这个问题
Hypothesis: $H = {cancer, \lnot {cancer}}$
Prior: $\pi(cancer) = 0.008$, $\pi (\lnot cancer) = 0.992$
L(D|h)

1
2
3

h   | pos  | neg
c   | 0.98 | 0.02
nc  | 0.03 | 0.97

右上角的是 false negative (negative result which is false)，又叫 miss
左下角的是 false positive (positive result which is false)，又叫 alarm
miss 和 alarm 两者是一个 tradeoff，如果永远都说是 cancer，那么没有任何 miss，却有很多的 alarm

计算：
$$
\begin{aligned}
P(c|D=pos) & = {\pi(c)L(pos|c) \over P(pos)} \\
& = {\pi(c)L(pos|c) \over \sum_i P(pos|h_i)P(h_i)} \\
& = {0.008*0.98 \over 0.008*0.98+0.992*0.03} \\
& = 0.208
\end{aligned}
$$

Example 2. Cancer cont.

如果第二次检验的结果还是 positive，那么该患者患癌症的几率有多大？

Method 1: Sequential apply of Baye’s Rules

前提是 $D1 \bot D2 |h$
此时的 Posterior:
$\pi(cancer) = 0.208$, $\pi (\lnot cancer) = 0.792$
H, L(D|h) = SAME
D2 = pos
$$
\begin{aligned}
P(c|D2=pos) & = {\pi(c)L(pos|c) \over P(pos)} \\
& = {0.208*0.98 \over 0.208*0.98+0.792*0.03} \\
& = 0.895
\end{aligned}
$$

每多做一次结果为 positive 的 test，最后的概率都会越大。

Method 2

1
2
3

h   |     ++    |     +-    |     -+    |    --     |
c   | 0.98*0.98 | 0.98*0.02 | 0.02*0.98 | 0.02*0.02 |
nc  | 0.03*0.03 | 0.03*0.97 | 0.97*0.03 | 0.97*0.97 |

Summary

Hypothesis H: a family of distributions indexed by $\ge $ 1 parameters

subjective because of prior
returns a whole distribution
$\theta_{map} = argmax P(\theta|D)$

Try to minimize MSE, $\theta_{mean}$
Try to minimize MAE, $\theta_{median}$

Hard bias: choices of H family
Soft bias: priors

Frequentist statistics

no notion of prior
focus on likelihood L(D|h)

MLP (Maximum likelihood principle)

Given L() function family & data, choose $$\theta = argmax \ L(D|\theta)$$

Example 1. Binomial distribution X~B(n,p)

X = {0,…n}
$$P(X=k)=\binom{n}{k}p^k(1-p)^{n-k}$$
Given n, and result of n flips -> k heads, how to estimate P?

简化
$$
\begin{aligned}
P_{ML} & = argmax \ L(k \ heads \ out \ of \ n \ flips | P) \\
& = argmax \binom {n}{k}P^k(1-P)^{n-k}\\
& = argmax \ klogP + (n-k)log(1-P)
\end{aligned}
$$

求导
=> $\int {dll \over dp} = k {1 \over p} - (n-k) {1 \over 1-p} = 0$
=> ${k \over p} = {n-k \over 1-p}$
=> $P_{ML} = {k \over n}$

Example 2.Gaussian

Fixed stdev, unkown mean X~N$(\mu \sigma^2)$
$$P(X=x)={1 \over \sqrt{2 \pi \sigma^2}} e^{-(x_i-\mu)^2 \over 2 \sigma^2}$$
Given $\sigma^2$ & data x1,…xn $ \in$ IR, drawn i,i,d (independently, identical distributed)

简化
$$
\begin{aligned}
\hat \mu_{ML} & = argmax \ \prod_i^n {1 \over \sqrt{2 \pi \sigma^2}} e^{-(x_i-\mu)^2 \over 2 \sigma^2} \\
& = argmax \sum_i^n {-(x_i - \mu)^2 \over 2 \sigma^2} \\
& = argmin \sum_i^n (x_i-\mu)^2
\end{aligned}
$$

求导
=> $\int {dll \over dp} = \sum_{i=1}^n 2(x_i-\mu)= 0$
=> $\sum_{i=1}^n x_i-n\mu$
=> $\mu_{ML} = {\sum_{i=1}^n \ x_i \over n} = \overline x_i$
=> sample mean = max likelihood gaussian true mean

Example 3. Linear regression

$$y = f(x_1,..x_n) + \epsilon$$

$$f(\overline x)=\sum_{j=1}^n \beta_jx_j$$
ASSUME

$\epsilon$~N $(\mu, \sigma^2)$
$\epsilon = y - f(x_1,…x_n)$ ~ N $(\mu, \sigma^2)$

简化
$$
\begin{aligned}
L(y_1, ….,y_n|x_1,…,x_n) & = \prod_i^n L(y_i|\overline x_i) \\
& = \prod {1 \over 2 \pi \sigma^2} e^{-(y_i-f(\overline x_i)^2) \over 2 \sigma^2}
\end{aligned}
$$

求导
$\hat \beta = argmax \sum_{i=1}^n {-(y_i - \overline x_i)^2 \over 2 \sigma^2}$
$= argmin \ \sum_{i=1}^n (y_i-f(\overline x_i)^2)$
$= MSE(mean \ squared \ error)$

=> MSE <=> Gaussian noise

Special case in Bayesian

$\pi(\theta) = constant$ (uniform prior)
=> $\theta_{MAP} = argmax \ \pi(\theta)L(D|\theta) = \theta_{ML}$

How to estimate P?

我们希望 Estimator

with enough data, should converge to the true value (asymptotical consistency)
fast converge to the right answer (efficiency)
low bias (usually no bias)
我们希望 $E[\hat \theta(D)]=\theta$。$bias(\hat \theta)=E[\hat \theta(D)]-\theta$ 这里我们想让它为 0，但是如果这是 ML inductive bias，我们不希望它为 0.
low variance (but can have high variants especially with little data)

MDL (minimum length description principle)

Encode 数据。比如说我们要传递 1-100 万之间的质数，那我们只用告诉对方这是质数，而不用把所有的质数列出来，如果我们要传递的是除了 2 和 3 的质数，那么我们要告诉对方这是质数，而且里面没有 2 和 3。
放到 machine learning 里，假设双方都有一堆数据 X1..Xn(X有若干属性(x11,x22…xnn)，我们要通讯的是 Y 也就是 X 的标签，我们可以按顺序传送，这需要很多的 bits，或者可以建立一个 decision tree，这个 tree 可以 classify 大多数的数据，把 tree + exceptions 发送给对方就好，可以节省很多 bits。
$h_{MDL}$ = argmin (bits to describe h + bits to describe exceptions)

Naive Bayes Classification

Goal

f: X -> Y <=> P(Y |X )
X = ⟨X1,X2 …,Xn⟩ n 个属性
Y = boolean value true or false

根据 Bayes rule, 来算 P(Y = yi|X)
$$P(Y=y_i|X=x_k)={P(X=x_k|Y=y_i)P(Y=y_i) \over \sum_j P(X=x_k|Y=y_j)P(Y=y_j)}$$

我们的目的是学习 P(Y|X)，来估计 P(X|Y) 和 P(Y)，用这些估计值，加上上面的 Bayes rule，就可以对新的 instance 分类。

Unbiased Learning of Bayes Classifiers is Impractical

Unbiased Learning of Bayes Classifiers 是不实际的，因为它要估计的参数太多，计算量太大。
当 Y is boolean and X is a vector of n boolean attributes 的情况下，我们为了得到 P(X|Y) 需要的估计的参数有：

$$θ_{ij} ≡P(X =x_i|Y =y_j)$$

i takes on $2^n$ possible values (one for each of the possible vector values of X )
j takes on 2 possible values (boolean)
=> $2^{n+1}$ parameters

For any fixed j, the sum over i of $θ_{ij}$ must be one.
i takes on $2^n-1$ possible values (one for each of the possible vector values of X )
j takes on 2 possible values (boolean)
=> $2(2^n-1)$ parameters

To obtain reliable estimates of each of these parameters, we will need to observe each of these distinct instances multiple times!

This is clearly unrealistic in most practical learning domains.

For example, if X is a vector containing 30 boolean features, then we will need to estimate more than 3 billion parameters.

Naive Bayes Algorithm

Naive Bayes 的优势在于它能让我们对 P(X|Y) 建模时用更少的参数，$2(2^n-1)$ -> 2n

Naive bayes assumption (Independence assumption)

Each $X_i$ is conditionally independent of each of the other $X_ks$ given Y, and also independent of each subset of the other $X_k$’s given Y.

在这个假设下，我们举个例子，X = ⟨X1,X2⟩ 时，可以得到

$$
\begin{aligned}
P(X|Y) & = P(X1,X2|Y) \\
& = P(X1|X2,Y)P(X2|Y) \\
& = P(X1|Y)P(X2|Y)
\end{aligned}
$$

更加 general 的形式 Factor L(|Y)
$$P(X1,X2…Xn|Y)=\prod_{i=1}^nP(X_i|Y)$$

同样的，Y and the Xi are boolean variables，这时候，我们只需要 2n 个参数来定义 $P(X_i = x_{ik}|Y = y_j)$!

首先我们产生 label，然后从 label 我们产生每一个属性。我们可以用下面的图来表示这种关系。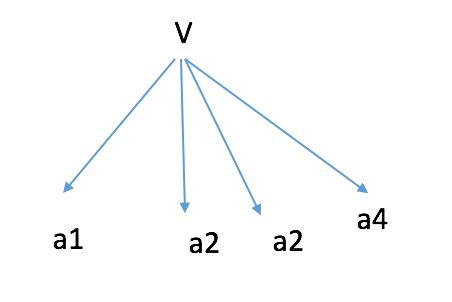

这个假设经常会被打破，然而即使是 horrible assumption，Naive Bayes 的效果也非常好。
tend to give extreme result

Derivation of Naive Bayes Algorithm

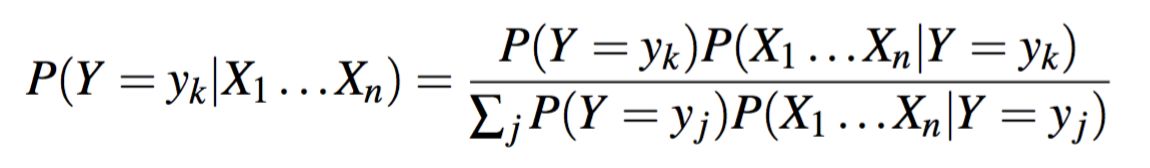
在 conditional independent assumption 下，可以继续得到
$$P(Y=y_k|X1…Xn)={P(Y=y_k)\prod_i P(X_i|Y=y_k) \over \sum_j P(Y=y_j)\prod_iP(Xi|Y=y_j)} \ (2)$$

$$Y \ <= \ argmax \ {P(Y=y_k)\prod_i P(X_i|Y=y_k) \over \sum_j P(Y=y_j)\prod_iP(Xi|Y=y_j)}$$

简化下就是
$$Y \ <= \ argmax \ P(Y=y_k)\prod_i P(X_i|Y=y_i=k) \ (3)$$

Naive Bayes for Discrete-Valued Inputs

Parameters

n input attributes Xi each take on J possible discrete values
Y: a discrete variable taking on K possible values

Learning task is to estimate two sets of parameters.
$$\theta_{ijk}≡P(X_i=x_{ij}|Y=y_k)$$

这需要 nJK 个参数，对每个 j,k value 都满足 $1 = \sum_j \theta_{ijk}$，也就是 n(J-1)K 个参数。

另外我们要定义 prior probability over Y
$$\pi_k=P(Y=y_k)$$
需要 K-1 个参数。

Estimate parameters

有两种估计参数的方法。Maximum likelihood 和 Bayesian MAP。

MLE: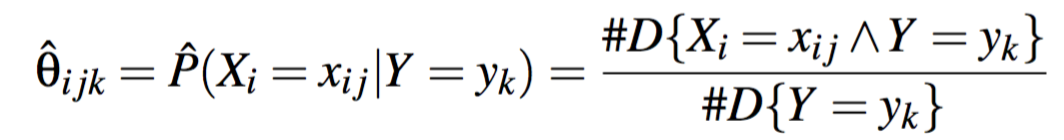

这种情况下有一个危险，当没有 example 符合条件的情况下，$\theta$ 可能为 0，所以我们需要 smooth。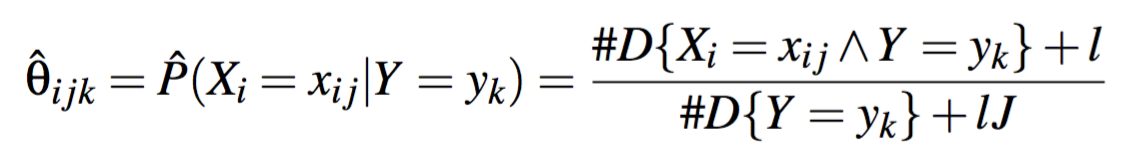

J: the number of distinct values Xi can take on
l: determines the strength of this smoothing

同样的，估计 $\pi_k$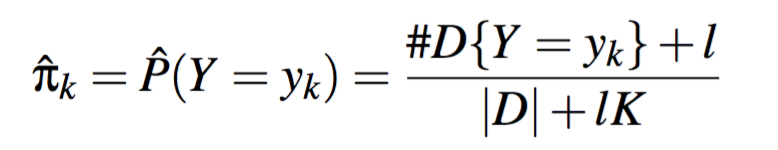

K: the number of distinct values Y can take on
l: determines the strength of the prior assumptions relative to the observed data D.

MAP classifier:
$Vmap = argmax P(v|a_1=x_1…a_n=x_n)=argmax P(v)L(a_1=x_1…a_n=x_n|v)$

为了估计 prior，我们需要 O(k) 个 parameter，这一般不是问题。
估计 L 的概率，我么需要 EXP(n) 个 parameter。

通过 Factor analysis 来减少 parameters

Naive Bayes for Continuous Inputs

当输入是连续的情况下，我们同样可以用(2)(3)来设计 Naive Bayes classifier，然而，由于 Xi 是连续的，我们必须用不同的方法来表示 P(Xi|Y) 的分布。通常的方法是假设 Xi 服从 Gaussian 分布，于是我们要定义 mean 和 standard deviation。

$$\mu_{ik}=E[X_i|Y=y_k]$$

$$\sigma^2_{ik}=E[(X_i-\mu_{ik})^2|Y=y_k]$$
这样我们需要估计 2nK 个参数。

prior:
$$\pi_k=P(Y=y_k)$$

Squashing

因为 independency 的假设，我们会得到非常极端的数值，如真实概率是 0.7, NB 出来的结果可能是 0.99999，真实概率是 0.2，NB 出来的结果可能是 0.0000001。
$$P^{\alpha}(y) \over \sum_i^n P^{\alpha}(y)$$

Naive Bayes Classifier vs Logistic Regression

LR is discriminative classifier as LR directly estimates the parameters of P(Y|X). We can view the distribution P(Y|X) as directly discriminating the value of the target value Y for any given instance X.
NB is generative classifier as NB directly estimates parameters for P(Y) and P(X|Y). We can view the distribution P(X|Y) as describing how to generat random instances X conditioned on the target attribute Y.
NB is with greater bias but lower variance than LR.

Algorithm

Naive_Bayes_Learn(examples)
For each target value vj
$\hat P(vj) <- estimate P(vj)$
For each attribute value ai of each attribute a
$\hat P(ai|vj) <- estimate P(ai|vj)$

Classifier_New_Instance(x)
$Vnb = argmax \hat P(vj)\prod \hat P(ai|vj)$

Example

new instance

$$Vnb = argmax \hat P(vj)\prod \hat P(ai|vj)$$

Learn Naive Bayes Text

算法

python 代码

运行命令

python nb.py split.train split.test

split.train / split.test 每行是一个 training file 文件名，有两个类别，con 和 lib。

con10.txt
con11.txt
con1.txt
con46.txt
con48.txt
con6.txt
lib16.txt
lib25.txt
lib28.txt
lib29.txt
lib2.txt
lib30.txt
lib31.txt
con25.txt
con39.txt

training file 每行是代表这个文件名类别的单词

Random
Jottings
October
30
2008
And
you

代码

import math
import sys
from collections import Counter
from sets import Set
# collect all distinct words and other tokens in examples
def initiate(file):
    global conDoc, libDoc, conCounter, libCounter
    conCounter, libCounter = Counter(), Counter()
    conDoc, libDoc = 0, 0
    f = open(file, 'r')
    files = f.readlines()
    for file in files:
        assert file.startswith('con') or file.startswith('lib')
        if file.startswith('con'):
            conDoc += 1
            conCounter = readTrain(file.strip(), conCounter, libCounter)
        else:
            libDoc += 1
            libCounter = readTrain(file.strip(), libCounter, conCounter)
def readTrain(trainFile, tokenDict, secondDict):
    f = open(trainFile, 'r')
    tokens = [line.strip().lower() for line in f]
    for token in tokens:
        tokenDict[token] += 1
        if token not in secondDict:
            secondDict[token] = 0
    return tokenDict
# calculate the requeired P(vj) and P(wk|vj)probability terms
def train(file):
    global conDoc, libDoc, conCounter, libCounter, priorCon, priorLib
    initiate(file)
    # P(vj) = docsj/examples
    priorCon = math.log(conDoc / float(conDoc + libDoc))
    priorLib = math.log(libDoc / float(conDoc + libDoc))
    # total number of words in Vocabulary
    vocLen = len(Set(conCounter.keys()).union(Set(libCounter.keys())))
    # P(wk|vj) = (nk+1)/(n+vocLen)
    conN = sum(conCounter.values()) + vocLen
    libN = sum(libCounter.values()) + vocLen
    conDefault = math.log(1.0 / conN)
    libDefault = math.log(1.0 / libN)
    for key in conCounter:
        conCounter[key] = math.log(
            float(conCounter[key] + 1) / conN)
    for key in libCounter:
        libCounter[key] = math.log(
            float(libCounter[key] + 1) / libN)
def test(file):
    global conDoc, libDoc, conCounter, libCounter, priorCon, priorLib
    testFile = open(file)
    testNum, correct = 0, 0
    for line in testFile:
        testNum += 1
        libProb = priorLib
        conProb = priorCon
        conProb, libProb = readTest(line.strip(), conProb, libProb)
        # print conProb,libProb
        if conProb > libProb:
            print 'C'
            if line.startswith('con'):
                correct += 1
        else:
            print 'L'
            if line.startswith('lib'):
                correct += 1
    accuracy = correct / float(testNum)
    print "Accuracy: %.04f" % accuracy
def readTest(file, conProb, libProb):
    global conCounter, libCounter
    f = open(file, 'r')
    tokens = [line.strip().lower() for line in f]
    for token in tokens:
        if token in conCounter:
            conProb += conCounter[token]
        if token in libCounter:
            libProb += libCounter[token]
    return conProb, libProb
if __name__ == "__main__":
    trainFile = sys.argv[1]
    testFile = sys.argv[2]
    train(trainFile)
    test(testFile)

Error and test of hypothesis

True error of hypothesis

sample error 和 true error 是不一样的。从 X 中抽取的样本 S，hypothesis h 关于 S 的 sample error 是 h 的实例在 S 中所在的比例，true error 也就是 true error 指的是对按某个分布随机抽取的实例，h 对它错误分类的概率。

h was wrong on 3/20 TEST ~ D
True error rate of $P(h(x)) \neq c(x)$ x ~ D

可能样本里只有一个 instance 错误，但是真实中会有很多这样的 input。

如果 $\hat \theta_{error} = 0.15$

Compare two hypothesis

计算 sample error 之间的差异，通过统计学理论计算。
$Err(h_A) ><= Err(h_B)$ => Err(h_B) - Err(h_A) > 0?
Depend on sample

Compare learning algorithms

La: training set -> $h_A$
Lb: training set -> $h_b$

Compare h_A(test set y) h_B(test set y)

better on this training set
avg performance of La is better than Lb

True error, E[Err_{test~D}[$L_A$(train ~ D)]] this is hypothesis