Hidden-Markov-Models

CMU 10601 的课程笔记。上一章讲了 Bayesian networks，我们发现它对 joint distributions 建模很有用，然而却不能解释 temporal/sequence models，也没法解释循环问题。所以需要引入另一个模型，隐马尔可夫模型（Hidden Markov Model，HMM）。HMM 用来描述一个含有隐含未知参数的马尔可夫过程。难点是从可观察的参数中确定该过程的隐含参数，然后利用这些参数来作进一步的分析。

Markov Process

要素

• States: 所有可能出现的状态。$S={S_0, S_1, …S_n}$
• Transition probabilities: 状态和状态间转换的概率。$P(q_t=S_i|q_{t-1}=S_j)$

假设
First order markov assumption
Transition probability depends only on current state
即 $P(q_t=S_i|q_{t-1}=S_j,q_{t-2}=S_k) = P(q_t=S_i|q_{t-1}=S_j) = a_{ji}$
$a_{ji} >=0 \ \forall j,i$ 且 $\sum_{i=0}^N a_{ji}=1 \ \forall j$
即 $q_t \bot q_j|q_{t-1} \ j<t-1$
即 Markov Process only remembers one state at a time 不具备记忆特质（memorylessness），条件概率仅仅与系统的当前状态相关，而与它的过去历史或未来状态，都是独立、不相关

$P(q_1….q_T) = \prod P(q_t|q1….q_{t-1}) = \prod P(q_t|q_{t-1})$

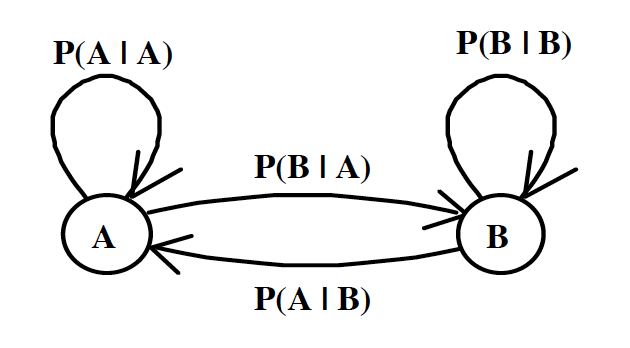
隐马尔可夫(HMM)

用途

• signal processing
• speech processing
• low level NLP: eg. POS tagging, phrase chunking, target information extraction

概念

用一个例子来描述吧，网上有一篇帖子讲的非常好，这里就直接引用过来了。

假设我手里有三个不同的骰子。第一个骰子是我们平常见的骰子（称这个骰子为 D6），6个面，每个面（1，2，3，4，5，6）出现的概率是1/6。第二个骰子是个四面体（称这个骰子为 D4），每个面（1，2，3，4）出现的概率是1/4。第三个骰子有八个面（称这个骰子为 D8），每个面（1，2，3，4，5，6，7，8）出现的概率是1/8。

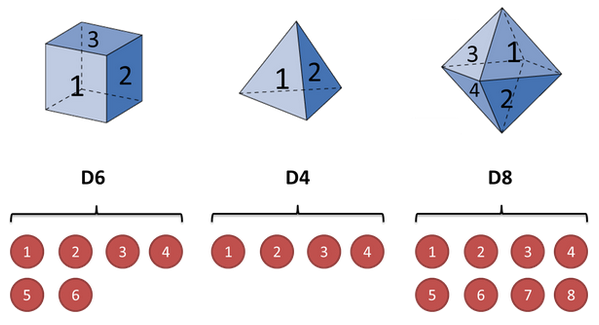
假设我们开始掷骰子，我们先从三个骰子里挑一个，挑到每一个骰子的概率都是1/3。然后我们掷骰子，得到一个数字，1，2，3，4，5，6，7，8中的一个。不停的重复上述过程，我们会得到一串数字，每个数字都是 1，2，3，4，5，6，7，8中的一个。例如我们可能得到这么一串数字（掷骰子10次）：1 6 3 5 2 7 3 5 2 4

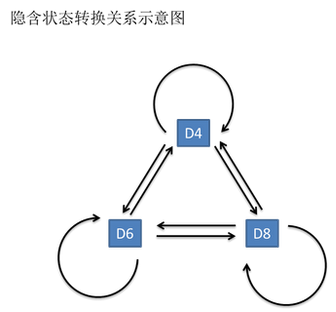
这串数字叫做可见状态链(observations)。但是在隐马尔可夫模型中，我们不仅仅有这么一串可见状态链，还有一串隐含状态链。在这个例子里，这串隐含状态链就是你用的骰子的序列。比如，隐含状态链有可能是：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8 (states)

一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率（transition probability）。在我们这个例子里，D6 的下一个状态是 D4，D6，D8 的概率都是1/3。D4，D8的下一个状态是 D4，D6，D8 的转换概率也都一样是 1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6 后面不能接 D4，D6 后面是 D6 的概率是0.9，是 D8 的概率是 0.1。这样就是一个新的 HMM。

同样的，尽管可见状态之间没有转换概率，但是隐含状态和可见状态之间有一个概率叫做输出概率（emission probability）。就我们的例子来说，六面骰（D6）产生 1 的输出概率是 1/6。产生 2，3，4，5，6 的概率也都是 1/6。我们同样可以对输出概率进行其他定义。比如，我有一个被赌场动过手脚的六面骰子，掷出来是1的概率更大，是 1/2，掷出来是 2，3，4，5，6 的概率是 1/10。

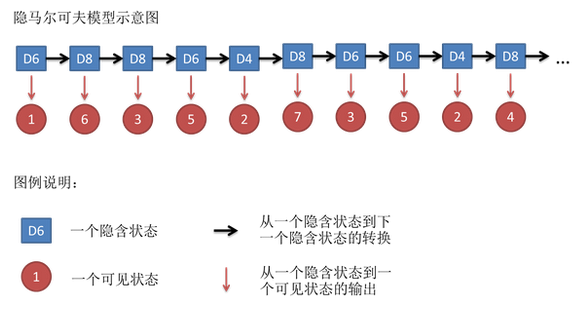
要素

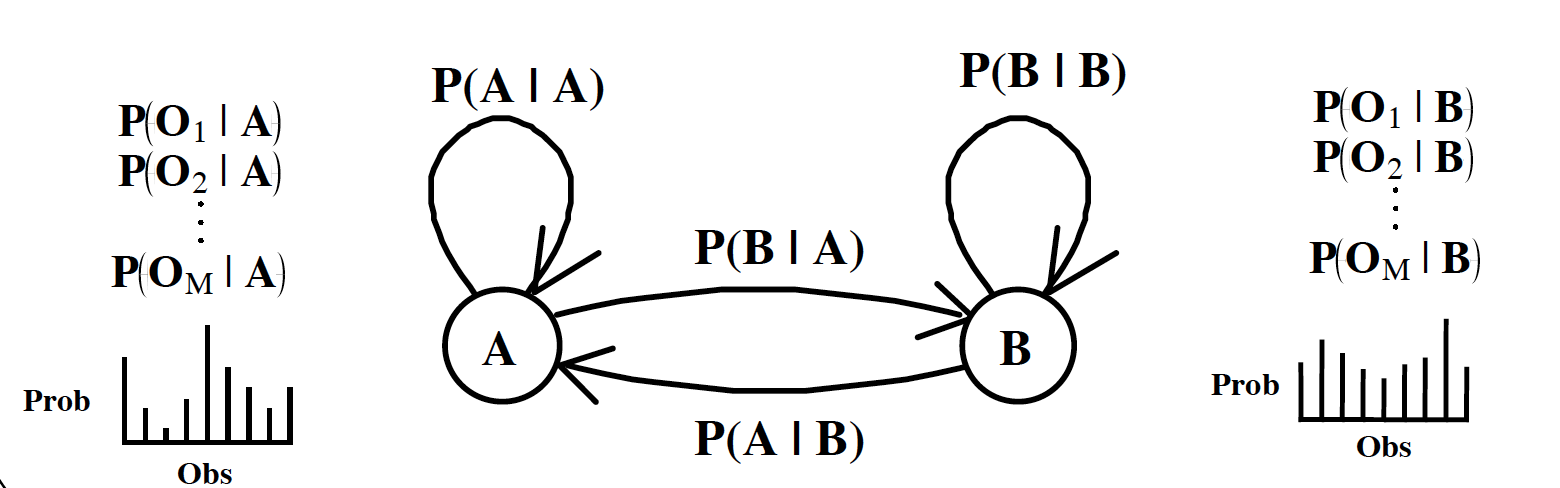
定义一些 notation。

• States(S): 隐含状态。$S={S_0, S_1, …S_n}$
• Transition probabilities(A): 状态和状态间转换的概率P(Si->Sj)。
  $P(q_t=S_i|q_{t-1}=S_j)=a_{ji}$
  n*n matrix of transition probabilities
• Emission probabilities(B) / Output prob distribution (at state j for symbol k): 发射概率（隐状态表现为显状态的概率）。状态 j 下，表现为 k 的概率。
  $P(y_t=O_k|q_t=S_j)=b_j(k)$
  n*m matrix of emission probabilities
• Observations: 观测序列(可见状态)。$O={O_0, O_1, …O_n}$
• Prior: 初始概率（隐状态）

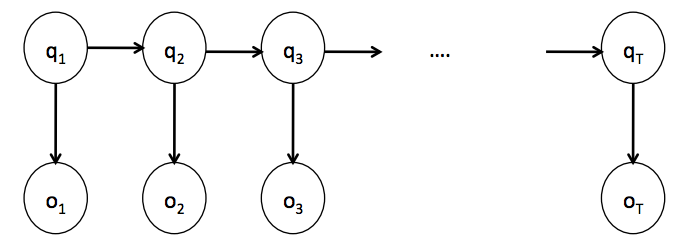
Probabilistic graphical models

HMM 的问题与解决

对于HMM来说，如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率，做模拟是相当容易的。但是应用 HMM 模型时候呢，往往是缺失了一部分信息的，有时候你知道骰子有几种，每种骰子是什么，但是不知道掷出来的骰子序列；有时候你只是看到了很多次掷骰子的结果，剩下的什么都不知道。如果应用算法去估计这些缺失的信息，就成了一个很重要的问题。和 HMM 模型相关的算法主要分为三类，分别解决三种问题。

Evaluation Problem

• Problem: Compute probability of observation sequence given a model $P(O|\lambda)$
  Given $\lambda, \overline O=O1,…Ot, => Calculate \ P(\overline O|\lambda)$
  知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道掷出这个结果的概率。
• Solution: Forward Algorithm, Viterbi Algorithm

问这个问题的目的在于检测观察到的结果是否和已知的模型吻合。如果很多次结果都对应了比较小的概率，那么就说明我们已知的模型很有可能是错的，有人偷偷把我们的骰子給换了。

Decoding Problem

• Problem: Find the state sequence Q which maximizes
  Given $\lambda = (A,B), \overline O=O1,…Ot, => Calculate $$\overline Q_{MAP}=argmax P(\overline Q|\overline O,\lambda)=argmax {P(\overline Q,\overline O|\lambda) \over P(\overline O|\lambda)} = argmax P(\overline Q,\overline O|\lambda)$
  知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道每次掷出来的都是哪种骰子（隐含状态链）。
• Solution: Viterbi Algorithm

这个问题其实有两种解法，会给出两个不同的答案。每个答案都对，只不过这些答案的意义不一样。第一种解法求最大似然状态路径，说通俗点呢，就是我求一串骰子序列，这串骰子序列产生观测结果的概率最大。第二种解法呢，就不是求一组骰子序列了，而是求每次掷出的骰子分别是某种骰子的概率。比如说我看到结果后，我可以求得第一次掷骰子是D4的概率是0.5，D6的概率是0.3，D8的概率是0.2.第一种解法我会在下面说到，但是第二种解法我就不写在这里了，如果大家有兴趣，我们另开一个问题继续写吧。

Training(Learning) Problem

• Problem: Adjust model parameters to maximize probability of observed sequences
  Given $\overline O=O1…Ot$ => Estimate $\hat \lambda_{ML} = argmax P(\overline O|\lambda)$
  知道骰子有几种（隐含状态数量），不知道每种骰子是什么（转换概率），观测到很多次掷骰子的结果（可见状态链），我想反推出每种骰子是什么（转换概率）。
• Solution: Forward-Backward Algorithm

这个问题很重要，因为这是最常见的情况。很多时候我们只有可见结果，不知道 HMM 模型里的参数，我们需要从可见结果估计出这些参数，这是建模的一个必要步骤。

Estimate A, B
$a_{ij_{ML}} = {\#(i->j) \over \#(i)}$ + SMOOTHING
$b_{j(Ok)_{ML}} = {\#(j \quad AND \quad Ok) \over \#(j)}$ + SMOOTHING

算法

Forward Algorithm 前向算法

$\alpha = P(O_1 O_2 … O_t, q_t = S_j|\lambda)$
基本逻辑是：穷举所有的骰子序列，还是计算每个骰子序列对应的概率，但是这回，把所有算出来的概率相加，得到的总概率就是我们要求的结果。
我们还需要一个 prior, 来表示 no states before 的情况。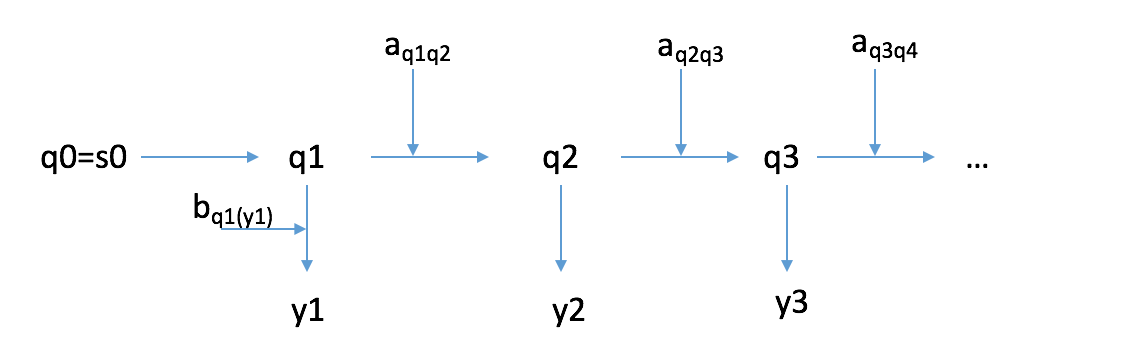

$P(\overline O|\lambda)=a_{q0q1}b_{q1(y1)}a_{q1q2}b_{q2(y2)}…a_{q_{t-1}qt}b_{qt(yt)}$
即 $P(\overline O|\lambda)=\sum_QP(\overline O,\overline Q|\lambda)$

递归的方法来计算 $\alpha$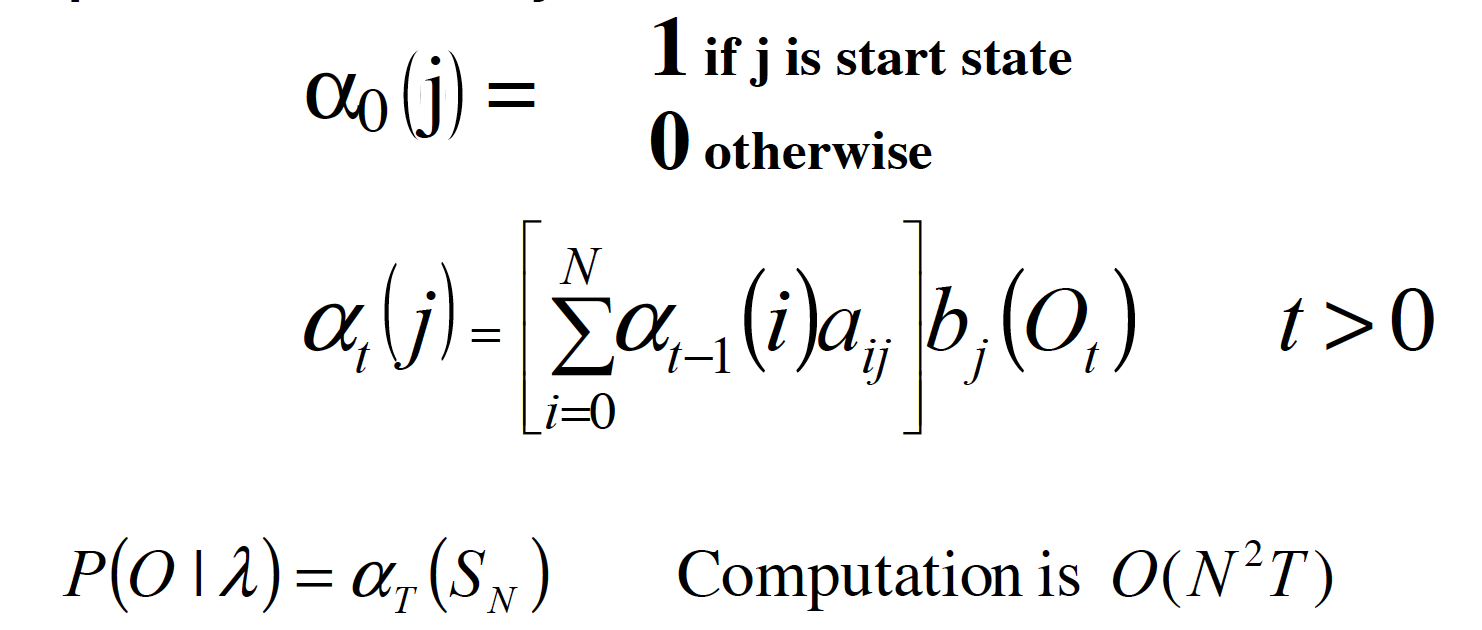

图解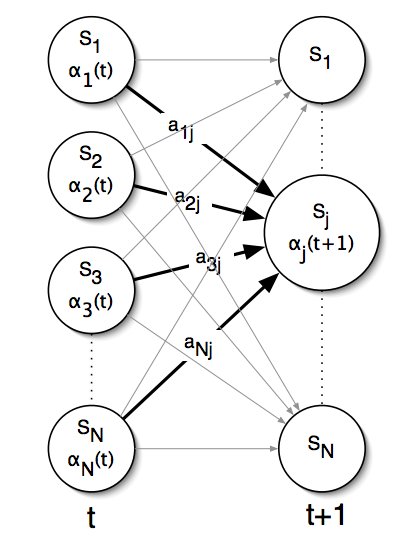

例子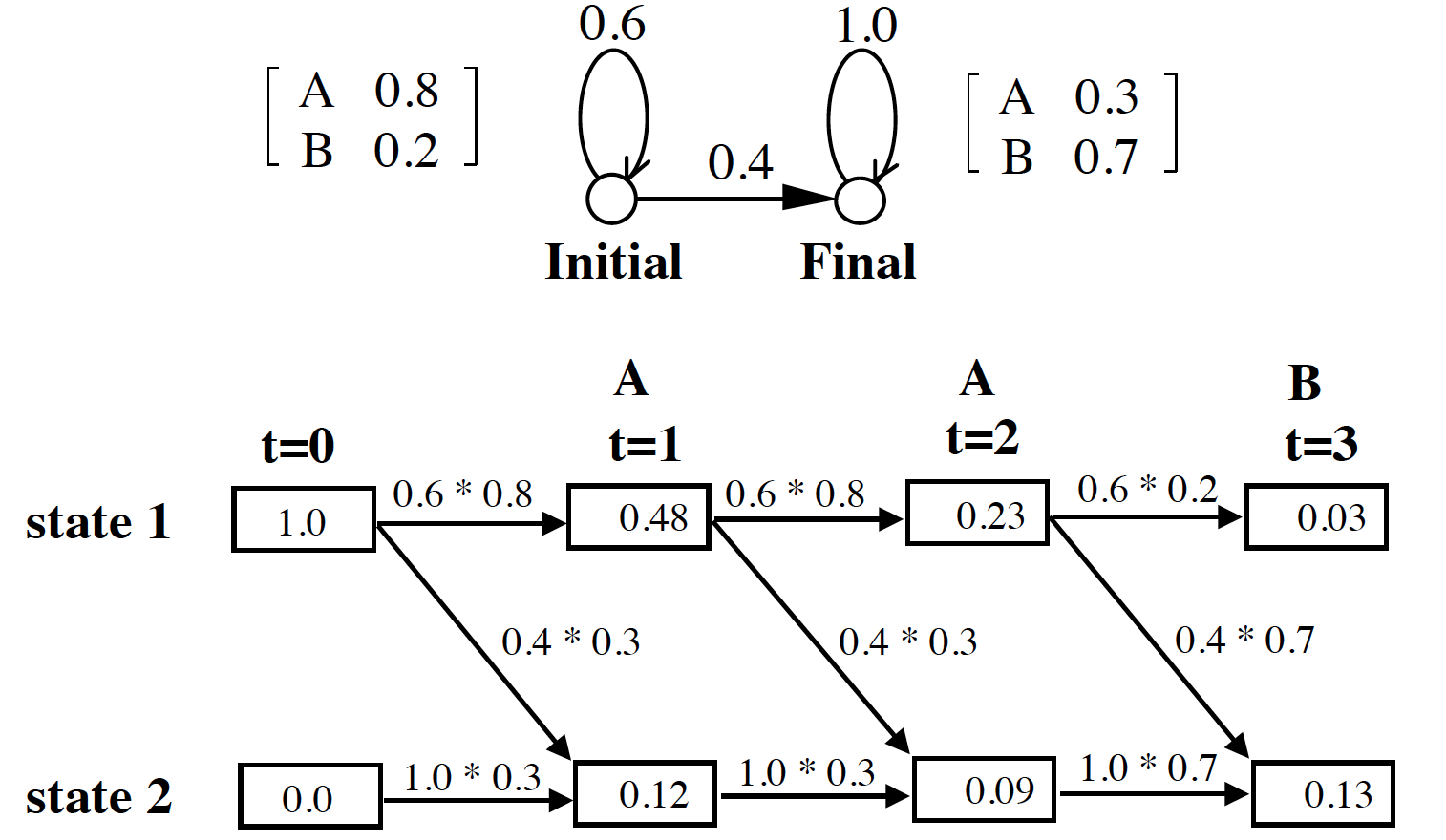

代码

from math import *
from logsum import log_sum
import sys


def initiate(transFile, emitFile, priorFile):
    global states, trans, emit, prior
    states, trans = probFileHandler(transFile)
    noUse, emit = probFileHandler(emitFile)
    prior = priorFileHandler(priorFile)
    # print 'states ', states
    # print 'trans ', trans
    # print 'prior ', prior


def probFileHandler(myFile):
    # states S
    S = []
    # transition or emit probability
    P = dict()
    # trans or emit
    f = open(myFile)
    for line in f:
        words = line.strip().split()
        S.append(words[0])
        d = dict([[words[i].split(':')[0], log(float(words[i].split(':')[1]))]
                  for i in range(1, len(words))])
        P[words[0]] = d
    return S, P


def priorFileHandler(myFile):
    f = open(myFile)
    prior = dict()
    for line in f:
        words = line.strip().split()
        prior[words[0]] = log(float(words[1]))
    return prior


def forward(word, alpha):
    global states, trans, emit, prior
    res = []
    # initial state
    if not alpha:
        for i in range(len(states)):
            curState = states[i]
            # use prior as trans_ji, at[j]*aji, use logsum
            res.append(prior[curState] + emit[curState][word])
    # if not initial state, iterate
    else:
        for i in range(len(states)):
            curState_i = states[i]
            for j in range(len(states)):
                curState_j = states[j]
                trans_ji = trans[curState_j][curState_i]
                if j == 0:
                    curRes = alpha[j] + trans_ji
                else:
                    # sum up all at[j]*aji, use logsum
                    curRes = log_sum(curRes, alpha[j] + trans_ji)
            # generate emit probability at t+1 at state i and multiply
            curRes += emit[curState_i][word]
            res.append(curRes)
    return res


def devFileHandler(myFile):
    f = open(myFile)
    for line in f:
        words = line.strip().split()
        alpha = []
        for word in words:
            alpha = forward(word, alpha)
        res = alpha[0]
        # P(O|lambda)=alphaT*(endingStateN)
        for i in range(1, len(alpha)):
            res = log_sum(res, alpha[i])
        print res


if __name__ == '__main__':
    devFile = sys.argv[1]
    transFile = sys.argv[2]
    emitFile = sys.argv[3]
    priorFile = sys.argv[4]
    initiate(transFile, emitFile, priorFile)
    devFileHandler(devFile)

Backward Algorithm

$\beta_t(i)=P(O_{t+1}O_{t+2}…O_T|q_t=S_i, \lambda)$

同样，递归的方法来计算 $\beta$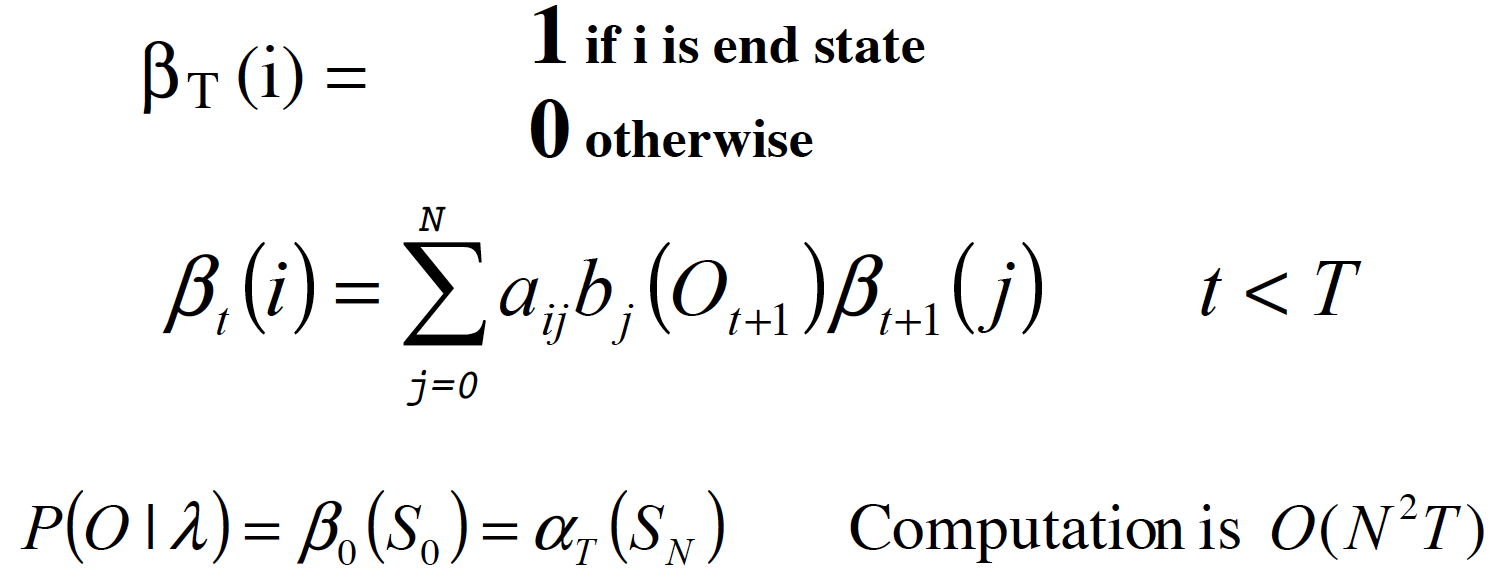

例子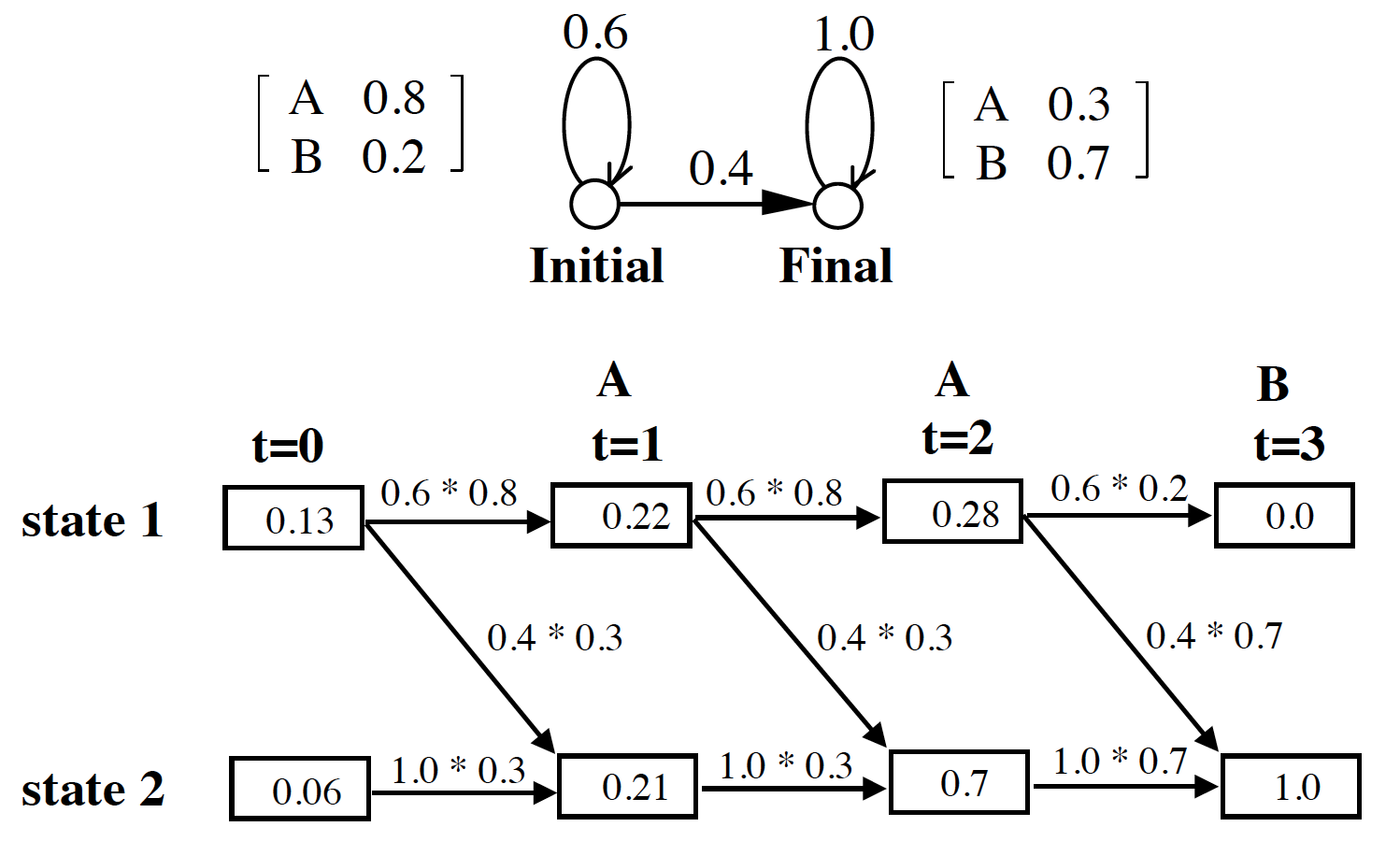

代码

from math import *
from logsum import log_sum
import sys


def initiate(transFile, emitFile, priorFile):
    global states, trans, emit, prior
    states, trans = probFileHandler(transFile)
    noUse, emit = probFileHandler(emitFile)
    prior = priorFileHandler(priorFile)
    # print 'states ', states
    # print 'trans ', trans
    # print 'prior ', prior


def probFileHandler(myFile):
    # states S
    S = []
    # transition or emit probability
    P = dict()
    # trans or emit
    f = open(myFile)
    for line in f:
        words = line.strip().split()
        S.append(words[0])
        d = dict([[words[i].split(':')[0], log(float(words[i].split(':')[1]))]
                  for i in range(1, len(words))])
        P[words[0]] = d
    return S, P


def priorFileHandler(myFile):
    f = open(myFile)
    prior = dict()
    for line in f:
        words = line.strip().split()
        prior[words[0]] = log(float(words[1]))
    return prior


def backward(word, beta):
    global states, trans, emit, prior
    res = []
    for i in range(len(states)):
        curState_i = states[i]
        for j in range(len(states)):
            curState_j = states[j]
            # transpose matrix!!!!
            trans_ij = trans[curState_i][curState_j]
            if j == 0:
                curRes = beta[j] + trans_ij + emit[curState_j][word]
            else:
                # sum up all at[j]*aji*emit[j], use logsum
                curRes = log_sum(
                    curRes, beta[j] + trans_ij + emit[curState_j][word])
        res.append(curRes)
    return res


def devFileHandler(myFile):
    f = open(myFile)
    for line in f:
        words = line.strip().split()
        # initialize, all states could be ending states
        beta = [0.0 for i in range(len(states))]

        for i in range(len(words) - 1, 0, -1):
            beta = backward(words[i], beta)

        res = prior[states[0]] + emit[states[0]][words[0]] + beta[0]

        for i in range(1, len(beta)):
            res = log_sum(res, prior[states[i]] +
                          emit[states[i]][words[0]] + beta[i])
        print res

if __name__ == '__main__':
    devFile = sys.argv[1]
    transFile = sys.argv[2]
    emitFile = sys.argv[3]
    priorFile = sys.argv[4]
    initiate(transFile, emitFile, priorFile)
    devFileHandler(devFile)

Viterbi Algorithm

Viterbi 被广泛应用到分词，词性标注等应用场景。和 Forward algorithm 差不多，两点改变：

1. 把 SUM 改成 MAX。
2. 记录 MAX 的h状态。

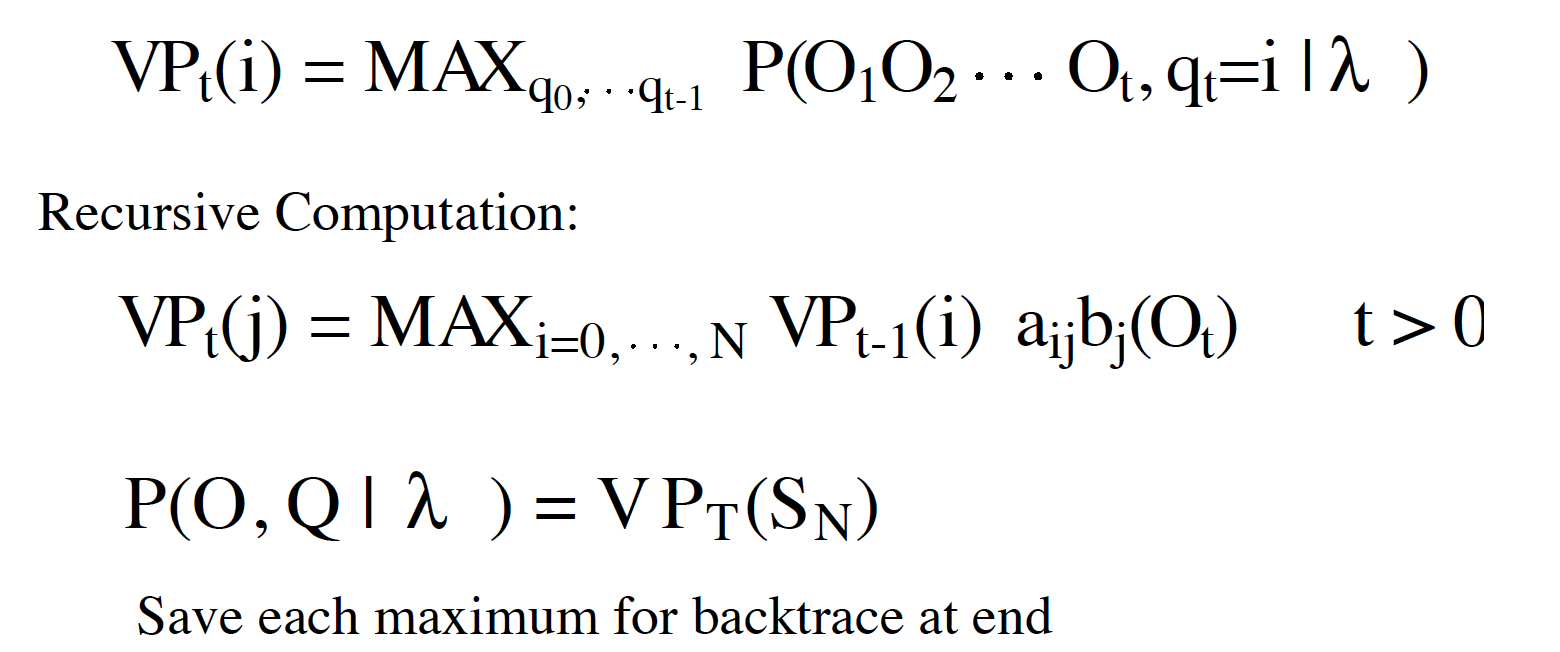
例子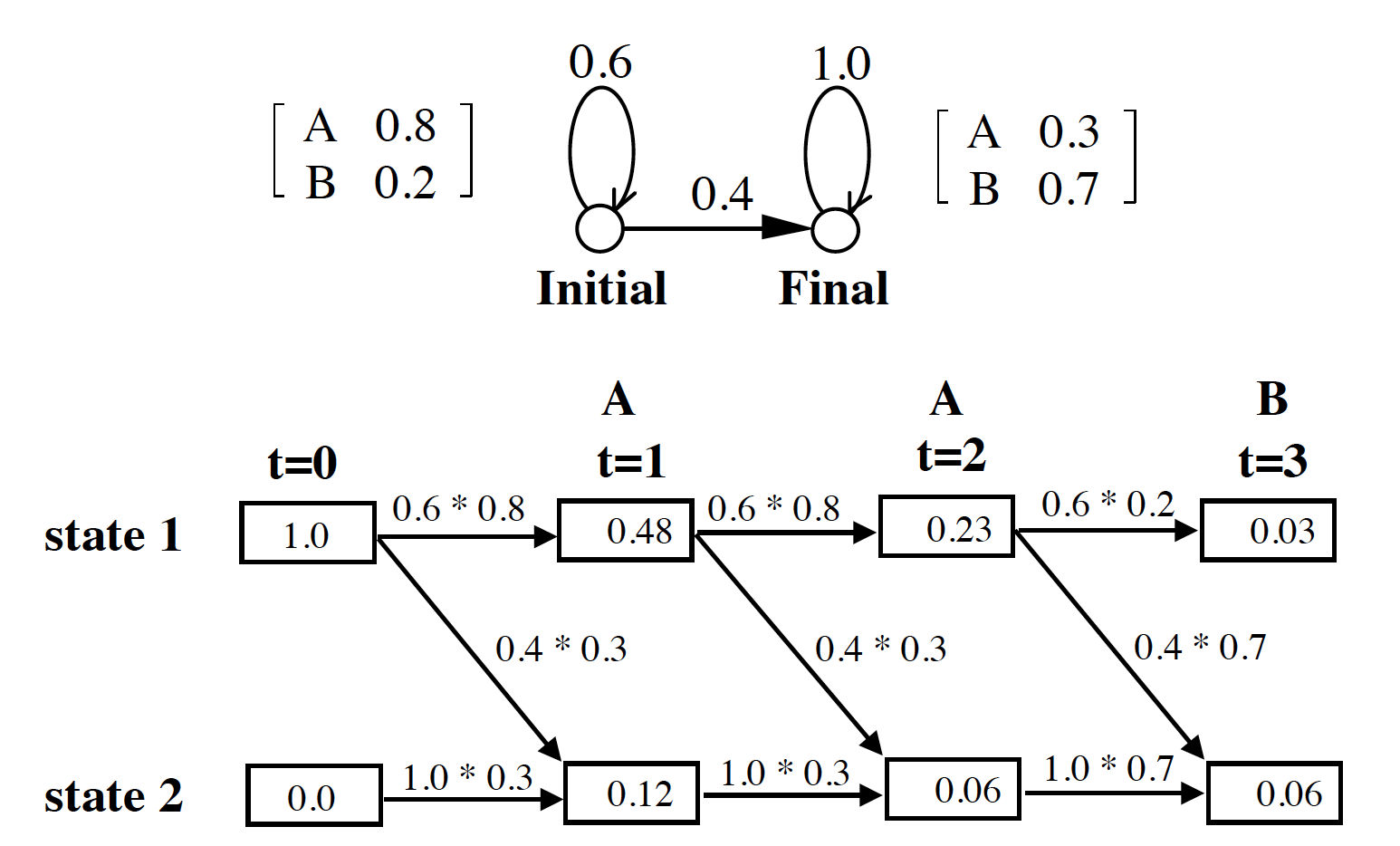

代码

from math import *
from logsum import log_sum
import sys
import copy


def initiate(transFile, emitFile, priorFile):
    global states, trans, emit, prior
    states, trans = probFileHandler(transFile)
    noUse, emit = probFileHandler(emitFile)
    prior = priorFileHandler(priorFile)
    # print 'states ', states
    # print 'trans ', trans
    # print 'prior ', prior


def probFileHandler(myFile):
    # states S
    S = []
    # transition or emit probability
    P = dict()
    # trans or emit
    f = open(myFile)
    for line in f:
        words = line.strip().split()
        S.append(words[0])
        d = dict([[words[i].split(':')[0], log(float(words[i].split(':')[1]))]
                  for i in range(1, len(words))])
        P[words[0]] = d
    return S, P


def priorFileHandler(myFile):
    f = open(myFile)
    prior = dict()
    for line in f:
        words = line.strip().split()
        prior[words[0]] = log(float(words[1]))
    return prior


def viterbi(word, alpha, resPath):
    global states, trans, emit, prior
    res = []
    curPath = []
    # initial state
    if alpha == []:
        for i in range(len(states)):
            curState = states[i]
            # use prior as trans_ji, at[j]*aji, use logsum
            res.append(prior[curState] + emit[curState][word])
            curPath.append([i])
    # if not initial state, iterate
    else:
        for i in range(len(states)):
            curState_i = states[i]
            curMaxIndex = 0
            for j in range(len(states)):
                curState_j = states[j]
                trans_ji = trans[curState_j][curState_i]
                if j == 0:
                    curMax = alpha[j] + trans_ji + emit[curState_i][word]
                else:
                    # sum up all at[j]*aji, use logsum
                    curRes = alpha[j] + trans_ji + emit[curState_i][word]
                    if curMax < curRes:
                        curMax = curRes
                        curMaxIndex = j
            # generate emit probability at t+1 at state i and multiply
            #curMax += emit[curState_i][word]
            res.append(curMax)
            # choose max
            curPath.append(copy.deepcopy(resPath[curMaxIndex]))
            curPath[i].append(i)
    return res, curPath


def devFileHandler(myFile):
    f = open(myFile)
    for line in f:
        words = line.strip().split()
        alpha = []
        resPath = []
        for word in words:
            alpha, resPath = viterbi(word, alpha, resPath)
        final = resPath[alpha.index(max(alpha))]
        for i in range(len(words)):
            print words[i] + '_' + states[final[i]],
        print

if __name__ == '__main__':
    devFile = sys.argv[1]
    transFile = sys.argv[2]
    emitFile = sys.argv[3]
    priorFile = sys.argv[4]
    initiate(transFile, emitFile, priorFile)
    devFileHandler(devFile)

Forward-Backward Algorithm

算法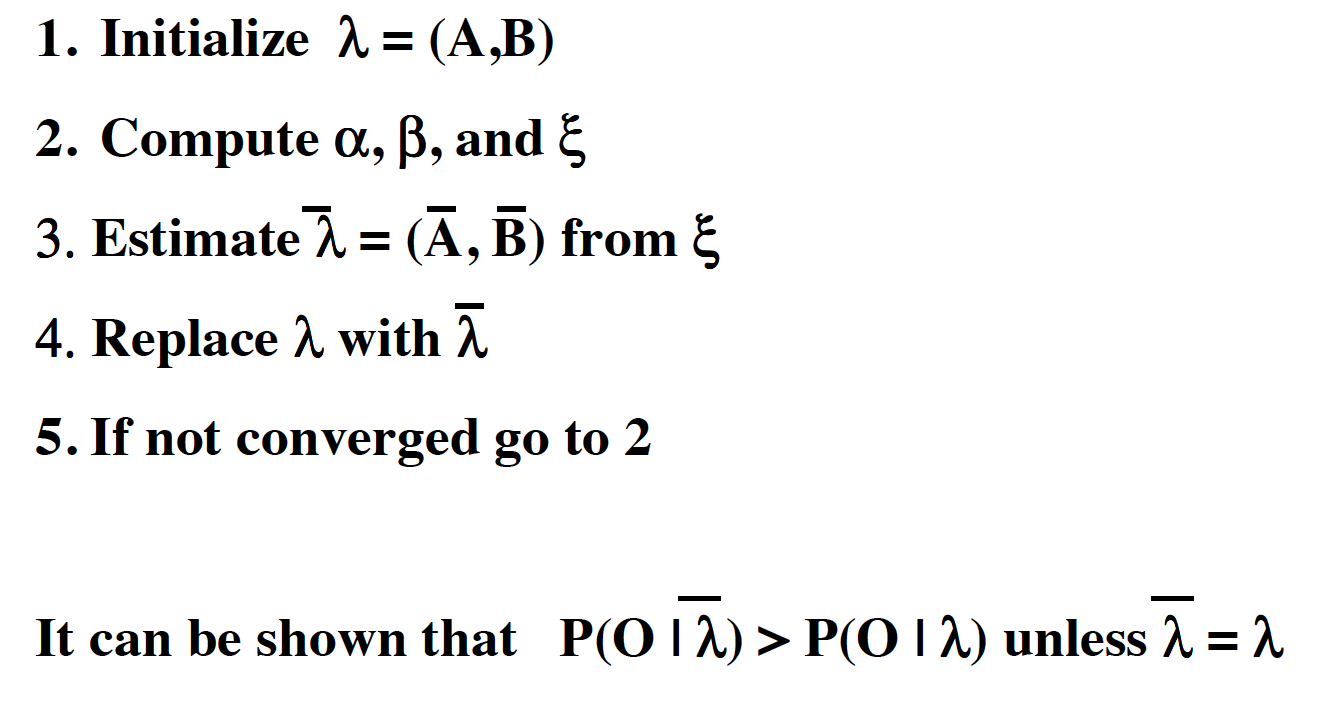

计算 $\alpha$, $\beta$,$\Xi$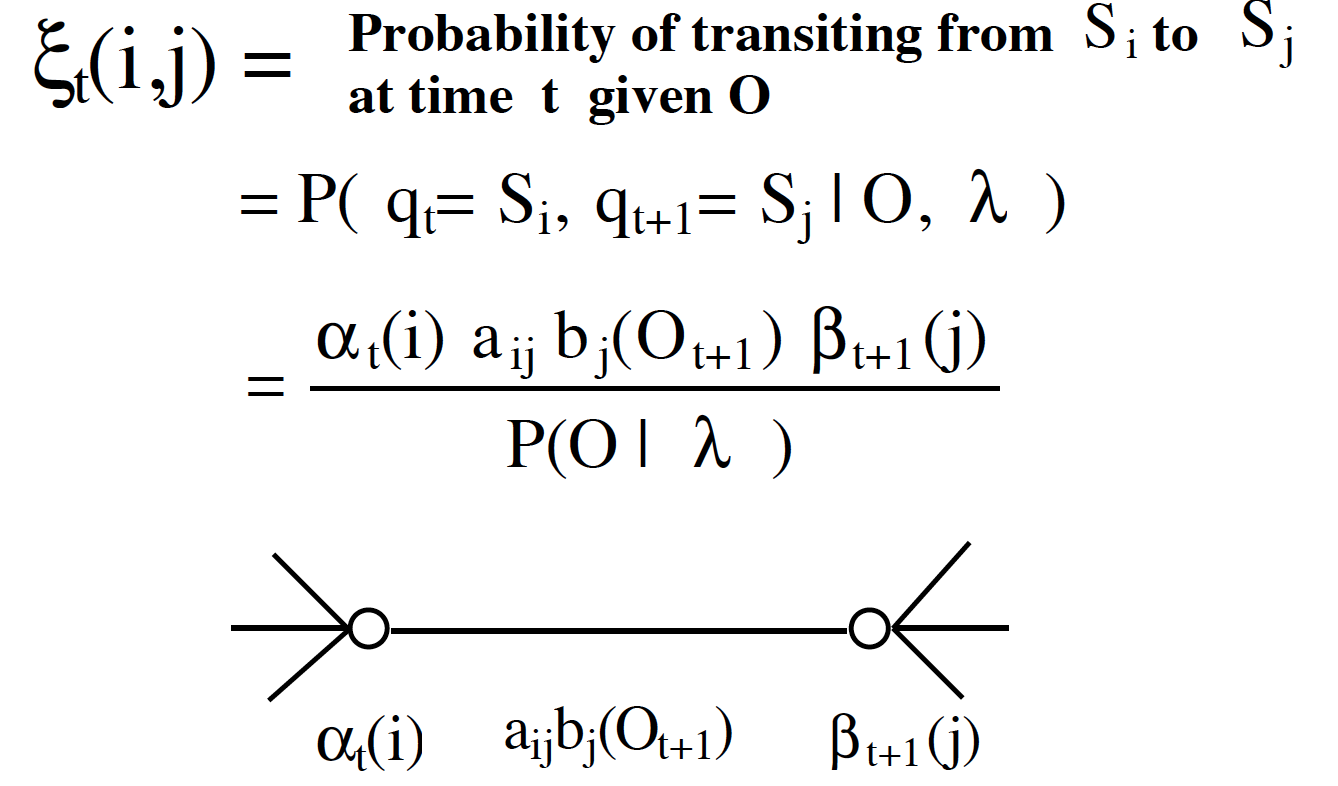

时间复杂度 O(NNT)

Baum-Welch Reestimation
估计 $\overline \lambda$

$$\overline a_{ij} = {expected \ number \ of \ trans \ from \ Si \ to \ Sj \over expected \ number \ of \ trans \ from \ Si}$$
=>

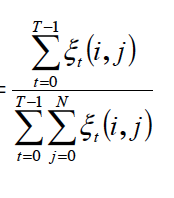
$$\overline b_{j(k)} = {expected \ number \ of \ times \ in \ state \ j \ with \ symbol \ k \over expected \ number \ of \ times \ in \ state \ j } $$

一文搞懂HMM（隐马尔可夫模型）