计算顺序: 从 loss 向输入传播
导数存储: 每层的导数 $(\Delta y, \Delta x)$ 结果进行存储,用于下一层导数的计算。
假设 $loss = ax_{1,t}+bx_{2,t}+cx_{3,t}+d-y$,当前参数 $m_0 = [a_0, b_0,c_0,d_0]$,那么计算梯度 $\Delta m=[x_{1,t}, x_{2,t}, x_{3,t}, 1]$,也就是分别求偏导。参数的更新为 $m:=m-\eta \Delta m$
下面的例子,黑色加深部分是前向计算的结果,我们的目的是求反向传播梯度。(原谅我 poor hand-writting :( )
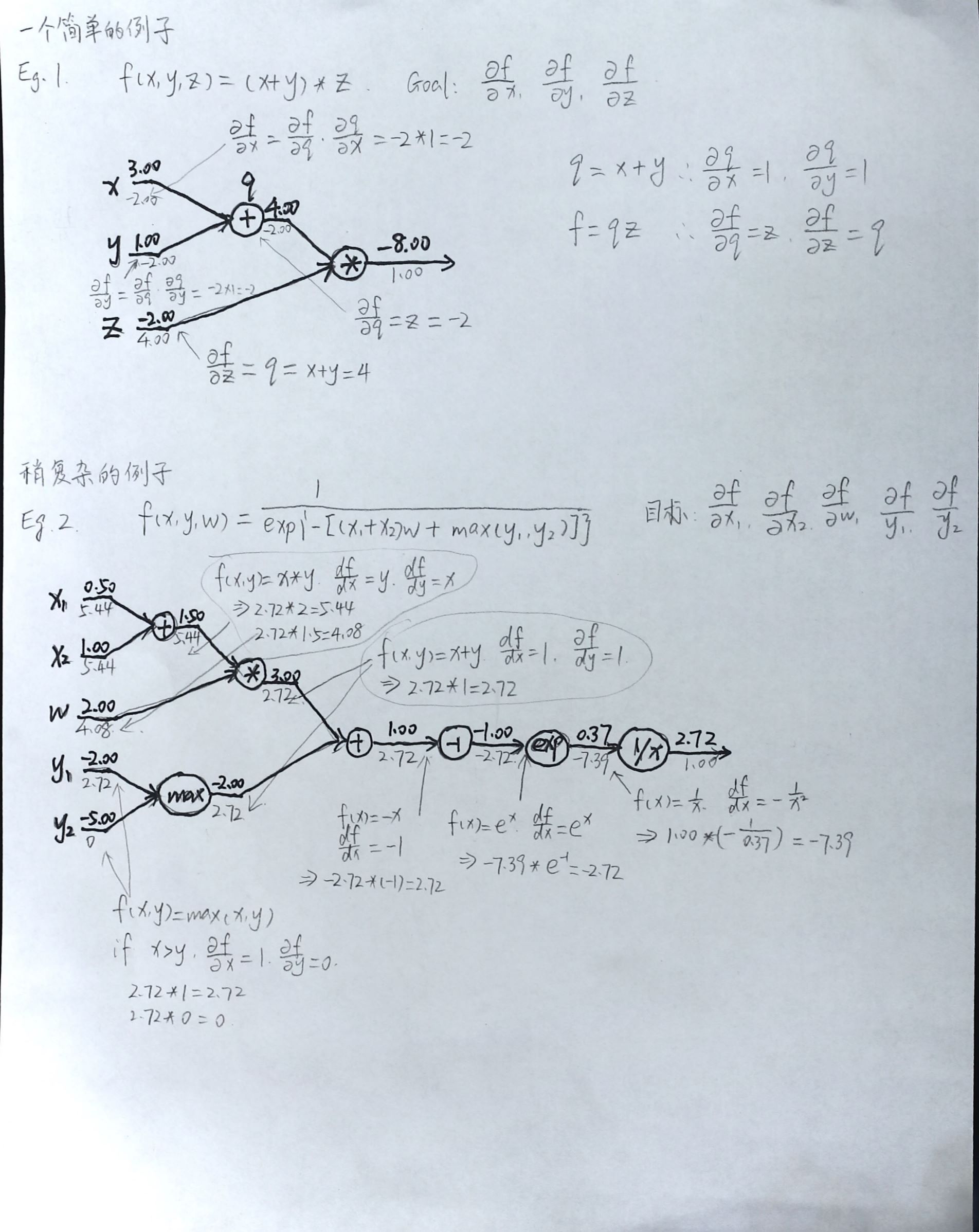
小结:
- 随机初始化参数
- 开启循环:t=0,1,2…
- 带入数据求出结果 $\hat y_t$
- 与真值比较得到 $loss=y-\hat y_t$
- 对各个变量求导得到 $\Delta m$
- 更新变量 m
- 如果 loss 足够小或者 t 循环结束,停止

