CMU 11642 的课程笔记。怎样评估 search engine 的效果?
Cranfield Methodology
- 获得 文档(documents) 集合
- 获得 信息需求(information needs) 集合
- 获得 相关性判断(relevance judgments)
- 计算(Measure) 各种方法找到相关文档的效果
- 比较(Compare) 各个方法的 effectiveness
所以有五个部分:
- 文档(documents)
- 信息需求(information needs)
- 相关性判断(relevance judgments)
- 指标(metrics)
- 对比(comparison of methods)
我们逐一来讨论
Test collections
documents, information needs, relevance judgements 三部分合起来称为一个 test collection。常用的 test collections 有
这些 test collections 都非常实用,然而都有各自的 bias。
Information Needs
一般来说,一个 test collection 有 50-200 个 information needs。information need 通常由 query 来体现,当然,也可以通过 search engines 中获得的 user behavior, user history, population behavior 来体现。那么,怎样获得 information needs 呢? 通常有三种办法。
- Ask 向用户询问他们要找什么,这当然是最优的方法。
- Observe 通过 search log,根据 query, clicks 等来观察用户需要什么,然后根据观察结果来还原 information needs。
- Guess 根据文档来猜这些文档能满足什么样的 information needs,这是 weakest option,但往往也是唯一的选择。
Relevance Assessment
人为判断,通常是主观的。
用不同的 techniques 检索出文档,然后人为判断每一种 technique 下的 top n 的文档,relevant set 就是这些判断为相关的文档的集合。
Metrics
Unranked Boolean Retrieval Model
P,R,P@n,F1 都是 set-based measures。适合 unranked boolean retrieval model,适合文本分类,然而对 ranked retrieval model 没那么适用。
Precision and Recall
$$Precision = {|Relevant \cap Retrieved| \over |Retrieved|} $$
$$Recall = {|Relevant \cap Retrieved| \over |Relevant|}$$
Precision-recall curve 呈现明显的锯齿形状,因为如果返回的第 k+1 篇文档不相关,那么在 k+1 篇文档位置上的 recall 和前 k 篇文档位置上的 recall 一样,但是 precision 显然下降。反之,如果返回的第 k+1 篇文档相关,那么 recall 和 precision 都会增大,这时候曲线会呈锯齿形上升。将这些细微的变化去掉通常采用差值
理论上来讲,整个文档集都会被 rank,然后对整个文档集来计算 P&R,然而这是没有必要的,所以引入了 P@n 和 MAP(Mean average precision)。
P@n
非常好理解,排名前 n 的文档的 precision。如 P@5,P@10。带来的问题是并没有对 query 的难度进行 normalize。简单的 query 可能会有更多的相关文档,难的 query 能得到的相关文档更少。所以 P@n 的 stability 不如 MAP.
F-Measure
对 precision 和 recall 进行 weight
$$F = {1 \over \alpha {1 \over P} + (1- \alpha) {1 \over R}}$$
如果 precision 和 recall 的权重相同,那就是 $F={2PR \over P+R}$
Average Results
Micro average across documents
每篇文档的重要性相同,具有许多相关文档的查询占主导地位,machine learning 常用, IR 不常用,因为 class distribution 更加的 skewed。
Macro average across queries
每个 query 的重要性相同,ad-hoc retrieval 最常用的 averaging method。
Ranked Retrieval
- Average Precision (AP)
- Mean Average Precision (MAP)
- Interpolated Average Precision
AP and MAP
MAP 是 single-value。AP 对单个需求,求返回结果中每篇相关文档位置上的 precision 的平均值。相当于某个 query 下对应的多条 precision-recall curve 下面积的平均值。对所有需求平均就能得到 MAP。MAP 可以在每个 recall 水平上提供单指标结果,具有非常好的 discrimination 和 stability。MAP 不需要选择固定的 recall 水平,也不需要插值,即使有些 query 的相关文档数很多而有些很少,最终的 MAP 显示每个 query 的作用却是相等的。单个系统在不同 information needs 的 MAP值相差较大(0.1-0.7),不同系统在同一 information need 上的 MAP 差异反而相对要小一些。
一道题解决。
看一下 AP 和 MAP 的分布。
MAP 用的非常多,一方面是因为它能很好的体现系统的优劣,一般来说,如果 MAP(A)>MAP(B),那么 A 系统更有可能比 B 系统好,像 P@n 等其它 metrics 就不能如此肯定。另外,MAP 计算很快,和 NDCG 相比。
MRR (Mean Reciprocal Rank)
有时候我们更关心第一篇相关文档。而排名较低的文档通常不会被浏览到。
Reciprocal rank 指的是 1/rank of first relevant document。所以 MRR 就是对所有需求的 RR 值求平均。

适用场景举例:某个学生想找 cmu 11642 的课程主页。
NDCG (Normalized Discounted Cumulative Gain)
Web search engines 中常用的方法。multi-valued relevance assessment,评估 ranking 的质量。
$$NDCG@k = Z_k \sum_{i=1}^k{2^{R_i}-1 \over log(1+i)}$$
- $R_i$ 指排名在 i 的相关文档的 relevance 分数
- $Z_k$ normalize,所以 NDCG@k=1 时是一个 perfect ranking。
$Z_k$ = 1/DCG@k for the “ideal” ranking
适用场景:可能有多个相关文档,且用户浏览文档的概率取决于页面的排名。eg. 顾客想要在网上买一台电脑,需要比较不同的型号、外观、价钱、排名。

RBP (Rank-Biased Precision)
非常简单的 model,对用户行为进行建模。multi-valued relevance assessments,用 user’s persistence 来评估 rank 质量。
$$RBP = (1-p) \sum_{i=1}^n R_ip^{i-1}$$
- p: user’s persistence
- n: 文档数量
- Ri: 第 i 篇文档的排名

trec-eval
ad-hoc retrieval 的标准的评估工具。
格式
Create test collections
- 收集大量的代表性文档(representative documents)
- 收集代表性信息需求(representative information needs),至少 25 条, 最好 50-100 条
- 把信息需求转换成 query 集合,一个信息需求至少要有两三个 query
- 在每个搜索引擎上运行 query,保存 top N 的文档,至少每个查询 50 篇文档
- 合并同一个信息需求的所有 query 在不同搜索引擎上的结果并随机排序
- 雇佣人员来判断文档相关性,保证一条信息需求下的所有文档必须由同一个人来判断。
Evaluation in a Dynamic Environment
Interleaved testing
- Input: 两个 rankings,分别由不同方法产生
- Output: 一个 ranking,由不同方法的所有 document 产生,一个好的 output 不会偏好任何一个方法。
Requirements:
- 用户不会注意到这一过程
- 对用户偏见不敏感
- 需要有反映用户偏好的用户行为
- 不应该改变用户的搜索体验
Procedure:
One trial
- 用户提交 query
- 搜索引擎选择两种排序方法(“A” and “B”),每种方法产生一个 document ranking
- 交替选择两种 document rankings
- 追踪 interleaved document ranking 的 click 情况
- 当用户停止点击的时候,根据被点击的文档给 “A” and “B” 两种方法分配 credit,确定在这一次 trial 中获胜的方法。
Repeat until enough trials are collected
Balanced interleaving
Assume that people read from top to bottom
假设:
- 用户从上往下浏览文档
- 用户会点击看起来合适的文档
- 当用户觉得已经满意了或者是失望了时,他们会停止浏览
- 每种方法(“A” and “B”)呈现文档的概率是相同的
- 用户(random clicker)点击的文档来自 “A” 或者 “B”的概率都是 50%
算法:
算法非常简单。首先决定从哪个方法开始,然后交替把文档加入 interleaved ranking,如果遇到了已经评估过的文档,就直接 counter++,但是不把文档加进 interleaved ranking 里。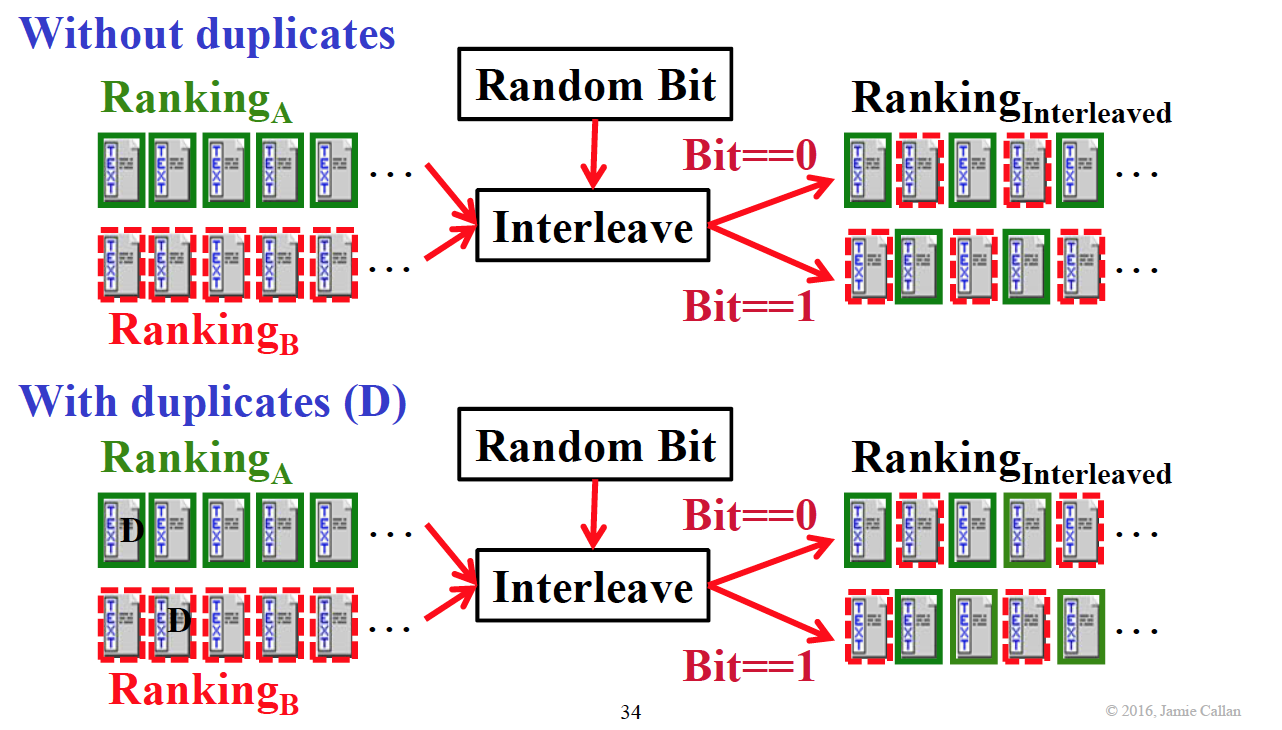
这样我们就得到了一个 ranking,然后我们还有一组数据是用户 click 的顺序。
$a_1,…,a_k$ 的集合与 $b_1,…b_k$ 的集合的并集包含了所有在 $i_1,…,i_{c_{max}}$ 中的文档,然后我们可以计算在 a’s top k 的点击数和 b’s top k 的点击数,得到最多 clicks 的方法获胜。
$$\Delta(A,B) = {wins(A)+0.5*ties(A,B) \over wins(A)+wins(B)+ties(A,B)}$$
E.g.,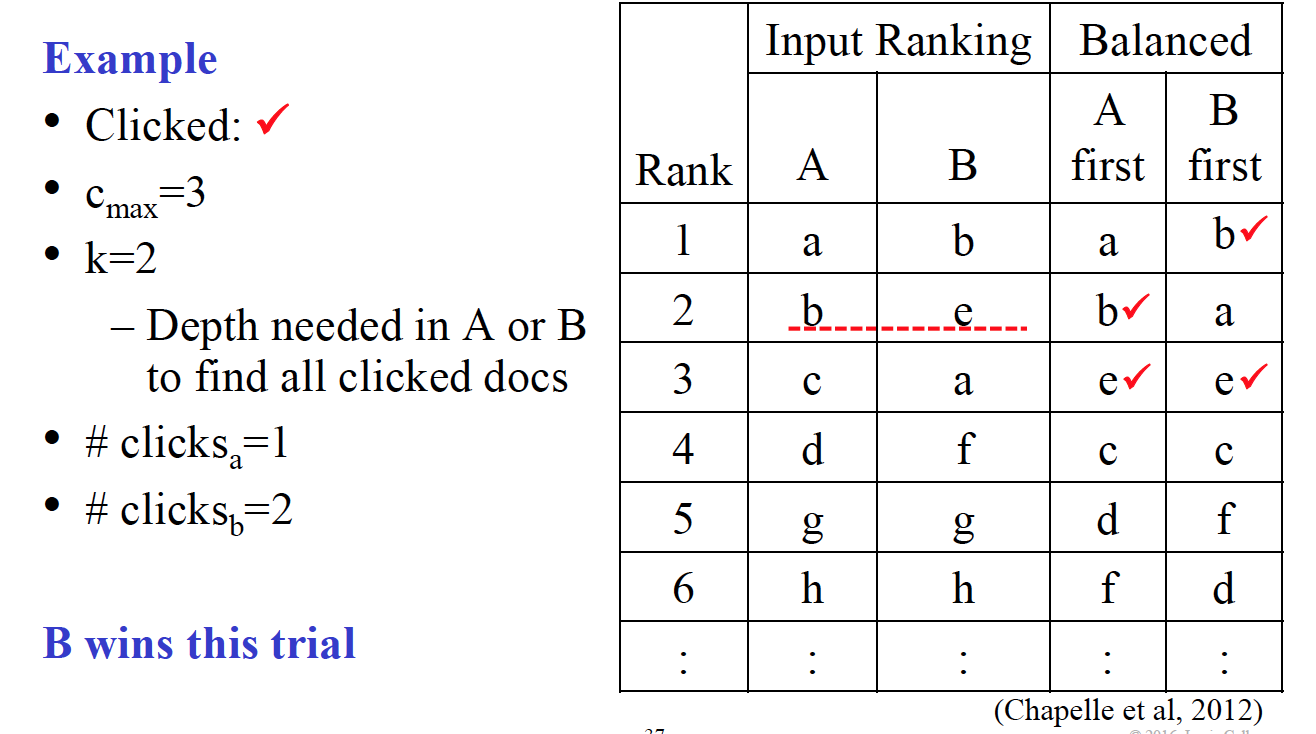
然而 Balanced-Interleaving 也可能带来意想不到的结果,如下图,假设用户随机点击了一个 result,那么有 3/4 的结果都是对 B 有利的,为什么?因为 3/4 的文档在 B 里的 ranking 都比 A 高!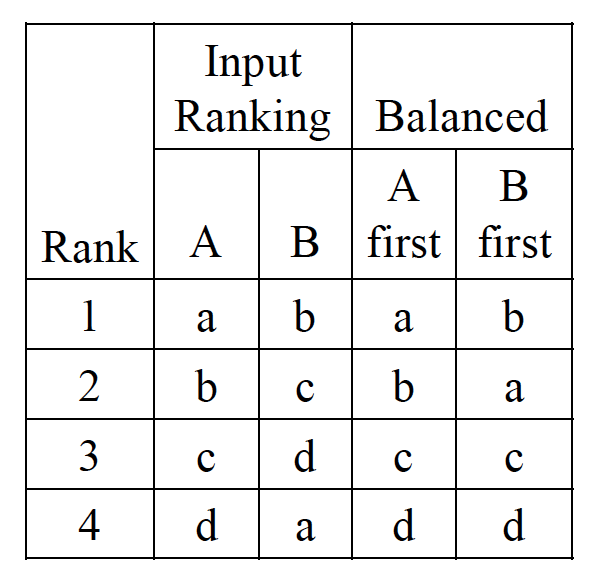
Team-draft interleaving
算法:
每一轮都随机产生先取哪种方法,如果有重复,跳过,取下一个。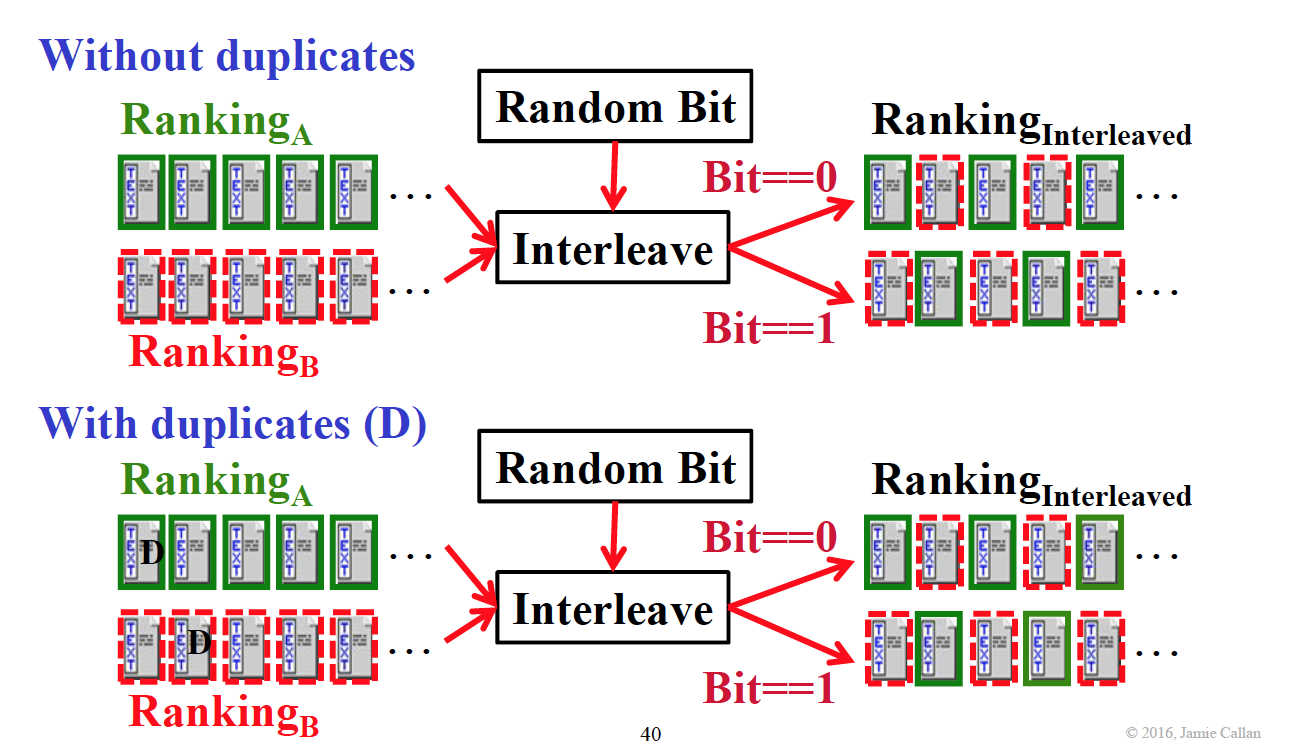
之后的步骤与 Balanced-Interleaving 相同。Team-draft 也可能产生难以预料的结果,如下图。
Metrics
- Abandonment rate: % of queries that receive no clicks
- Reformulation rate: % of queries that are reformulated
- Queries per session: Session == Information need
- Clicks per query, Clicks@1
- pSAT-clicks: % of documents with dwell time > 30 seconds
- pSkip: % of documents that are skipped
- Max Reciprocal Rank, Mean Reciprocal Rank
- Time to First Click, Time to Last Click
Cranfield vs. Interleaving
一般来说,我们更多的会使用 Cranfield,因为
- Cranfield 更成熟,已经使用了很多年而且易于理解
- Cranfield 支持大量的 metrics,能提供更多关于 ranking behavior 的信息
- Cranfield 几乎在所有场景下都使用,而 Interleaving 需要有 query traffic
尽管如此,interleaving 仍然是一个很有用的工具,在下面的条件下可以使用。
- Inexpensive, adaptive, sensitive to small differences


